Timeseries anomaly detection using an Autoencoder
Source:vignettes/examples/timeseries/timeseries_anomaly_detection.Rmd
timeseries_anomaly_detection.RmdIntroduction
This script demonstrates how you can use a reconstruction convolutional autoencoder model to detect anomalies in timeseries data.
Setup
library(dplyr, warn.conflicts = FALSE)
library(ggplot2)
theme_set(theme_minimal())
library(listarrays)
library(tfdatasets, exclude = c("shape"))
library(keras3)Load the data
We will use the Numenta Anomaly Benchmark(NAB) dataset. It provides artificial timeseries data containing labeled anomalous periods of behavior. Data are ordered, timestamped, single-valued metrics.
We will use the art_daily_small_noise.csv file for
training and the art_daily_jumpsup.csv file for testing.
The simplicity of this dataset allows us to demonstrate anomaly
detection.
get_data <- function(url_suffix) {
url_root <- "https://raw.githubusercontent.com/numenta/NAB/master/data/"
url <- paste0(url_root, url_suffix)
file <- get_file(origin = url) # cache file locally
# parse csv; 2 columns with types: datetime (T), double (d)
readr::read_csv(file, col_types = "Td")
}
df_small_noise <- get_data("artificialNoAnomaly/art_daily_small_noise.csv")
df_daily_jumpsup <- get_data("artificialWithAnomaly/art_daily_jumpsup.csv")Quick look at the data
df_small_noise## # A tibble: 4,032 × 2
## timestamp value
## <dttm> <dbl>
## 1 2014-04-01 00:00:00 18.3
## 2 2014-04-01 00:05:00 22.0
## 3 2014-04-01 00:10:00 18.6
## 4 2014-04-01 00:15:00 22.0
## 5 2014-04-01 00:20:00 21.9
## 6 2014-04-01 00:25:00 21.2
## 7 2014-04-01 00:30:00 20.6
## 8 2014-04-01 00:35:00 20.3
## 9 2014-04-01 00:40:00 21.5
## 10 2014-04-01 00:45:00 19.2
## # ℹ 4,022 more rows
df_daily_jumpsup## # A tibble: 4,032 × 2
## timestamp value
## <dttm> <dbl>
## 1 2014-04-01 00:00:00 19.8
## 2 2014-04-01 00:05:00 20.5
## 3 2014-04-01 00:10:00 20.0
## 4 2014-04-01 00:15:00 21.5
## 5 2014-04-01 00:20:00 20.2
## 6 2014-04-01 00:25:00 19.9
## 7 2014-04-01 00:30:00 21.7
## 8 2014-04-01 00:35:00 20.9
## 9 2014-04-01 00:40:00 18.4
## 10 2014-04-01 00:45:00 18.7
## # ℹ 4,022 more rowsVisualize the data
Timeseries data without anomalies
We will use the following data for training.
plot_ts <- function(df) {
ggplot(df, aes(x = timestamp, y = value)) + geom_line() +
scale_x_datetime(date_breaks = "1 day", date_labels = "%b-%d")
}
plot_ts(df_small_noise) + ggtitle("Without Anomaly")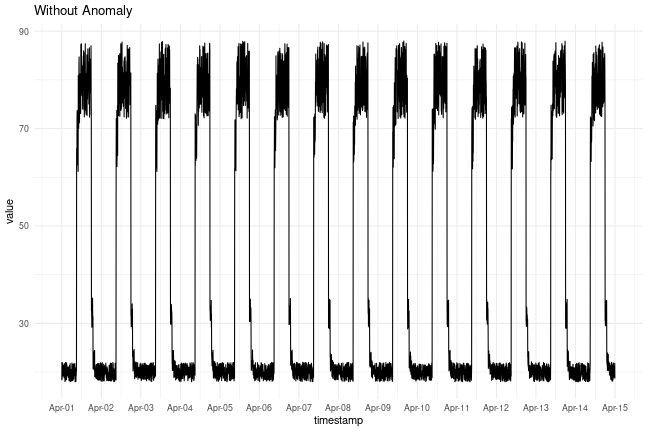
plot of chunk unnamed-chunk-4
Timeseries data with anomalies
We will use the following data for testing and see if the sudden jump up in the data is detected as an anomaly.
plot_ts(df_daily_jumpsup) + ggtitle("With Anomaly")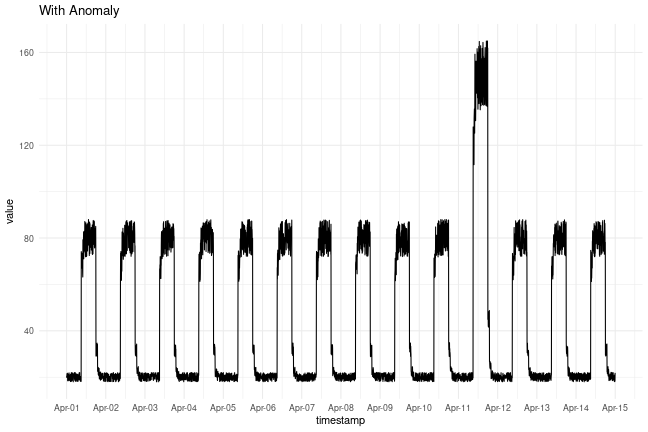
plot of chunk unnamed-chunk-5
Prepare training data
Get data values from the training timeseries data file and normalize
the value data. We have a value for every 5
mins for 14 days.
- 24 * 60 / 5 = 288 timesteps per day
- 288 * 14 = 4032 data points in total
df_train <- df_small_noise |>
mutate(value = (value - mean(value)) / sd(value))
cat("Number of training samples:", nrow(df_train), "\n")## Number of training samples: 4032Create sequences
Create sequences combining TIME_STEPS contiguous data
values from the training data.
TIME_STEPS <- 288
as_dataset <- function(df) {
x <- as.matrix(df$value)
ds <- timeseries_dataset_from_array(x, NULL, sequence_length = TIME_STEPS)
# Because the dataset is small, cast TF Dataset to an R array for convenience.
ds |> as_array_iterator() |> iterate() |> bind_on_rows()
}
x_train <- as_dataset(df_train)
writeLines(sprintf("Training input shape: (%s)", toString(dim(x_train))))## Training input shape: (3745, 288, 1)Build a model
We will build a convolutional reconstruction autoencoder model. The
model will take input of shape
(batch_size, sequence_length, num_features) and return
output of the same shape. In this case, sequence_length is
288 and num_features is 1.
model <- keras_model_sequential(input_shape = c(TIME_STEPS, 1)) |>
layer_conv_1d(
filters = 32, kernel_size = 7, padding = "same",
strides = 2, activation = "relu"
) |>
layer_dropout(rate = 0.2) |>
layer_conv_1d(
filters = 16, kernel_size = 7, padding = "same",
strides = 2, activation = "relu"
) |>
layer_conv_1d_transpose(
filters = 16, kernel_size = 7, padding = "same",
strides = 2, activation = "relu"
) |>
layer_dropout(rate = 0.2) |>
layer_conv_1d_transpose(
filters = 32, kernel_size = 7, padding = "same",
strides = 2, activation = "relu"
) |>
layer_conv_1d_transpose(filters = 1, kernel_size = 7, padding = "same")
model |> compile(optimizer=optimizer_adam(learning_rate=0.001), loss="mse")
model## Model: "sequential"
## ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
## ┃ Layer (type) ┃ Output Shape ┃ Param # ┃
## ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
## │ conv1d (Conv1D) │ (None, 144, 32) │ 256 │
## ├─────────────────────────────────┼────────────────────────┼───────────────┤
## │ dropout (Dropout) │ (None, 144, 32) │ 0 │
## ├─────────────────────────────────┼────────────────────────┼───────────────┤
## │ conv1d_1 (Conv1D) │ (None, 72, 16) │ 3,600 │
## ├─────────────────────────────────┼────────────────────────┼───────────────┤
## │ conv1d_transpose │ (None, 144, 16) │ 1,808 │
## │ (Conv1DTranspose) │ │ │
## ├─────────────────────────────────┼────────────────────────┼───────────────┤
## │ dropout_1 (Dropout) │ (None, 144, 16) │ 0 │
## ├─────────────────────────────────┼────────────────────────┼───────────────┤
## │ conv1d_transpose_1 │ (None, 288, 32) │ 3,616 │
## │ (Conv1DTranspose) │ │ │
## ├─────────────────────────────────┼────────────────────────┼───────────────┤
## │ conv1d_transpose_2 │ (None, 288, 1) │ 225 │
## │ (Conv1DTranspose) │ │ │
## └─────────────────────────────────┴────────────────────────┴───────────────┘
## Total params: 9,505 (37.13 KB)
## Trainable params: 9,505 (37.13 KB)
## Non-trainable params: 0 (0.00 B)Train the model
Please note that we are using x_train as both the input
and the target since this is a reconstruction model.
history = model |> fit(
x_train, x_train,
epochs = 50,
validation_split = 0.1,
callbacks = c(
callback_early_stopping(
monitor = "val_loss", patience = 5, mode = "min"
)
)
)## Epoch 1/50
## 106/106 - 6s - 55ms/step - loss: 0.1863 - val_loss: 0.0316
## Epoch 2/50
## 106/106 - 0s - 2ms/step - loss: 0.0333 - val_loss: 0.0233
## Epoch 3/50
## 106/106 - 0s - 4ms/step - loss: 0.0248 - val_loss: 0.0201
## Epoch 4/50
## 106/106 - 0s - 2ms/step - loss: 0.0209 - val_loss: 0.0187
## Epoch 5/50
## 106/106 - 0s - 2ms/step - loss: 0.0179 - val_loss: 0.0147
## Epoch 6/50
## 106/106 - 0s - 2ms/step - loss: 0.0150 - val_loss: 0.0113
## Epoch 7/50
## 106/106 - 0s - 2ms/step - loss: 0.0127 - val_loss: 0.0094
## Epoch 8/50
## 106/106 - 0s - 2ms/step - loss: 0.0109 - val_loss: 0.0088
## Epoch 9/50
## 106/106 - 0s - 2ms/step - loss: 0.0096 - val_loss: 0.0083
## Epoch 10/50
## 106/106 - 0s - 2ms/step - loss: 0.0086 - val_loss: 0.0070
## Epoch 11/50
## 106/106 - 0s - 2ms/step - loss: 0.0078 - val_loss: 0.0061
## Epoch 12/50
## 106/106 - 0s - 3ms/step - loss: 0.0073 - val_loss: 0.0057
## Epoch 13/50
## 106/106 - 0s - 2ms/step - loss: 0.0068 - val_loss: 0.0053
## Epoch 14/50
## 106/106 - 0s - 2ms/step - loss: 0.0064 - val_loss: 0.0050
## Epoch 15/50
## 106/106 - 0s - 2ms/step - loss: 0.0061 - val_loss: 0.0045
## Epoch 16/50
## 106/106 - 0s - 2ms/step - loss: 0.0058 - val_loss: 0.0040
## Epoch 17/50
## 106/106 - 0s - 2ms/step - loss: 0.0056 - val_loss: 0.0041
## Epoch 18/50
## 106/106 - 0s - 2ms/step - loss: 0.0053 - val_loss: 0.0035
## Epoch 19/50
## 106/106 - 0s - 3ms/step - loss: 0.0050 - val_loss: 0.0037
## Epoch 20/50
## 106/106 - 0s - 2ms/step - loss: 0.0048 - val_loss: 0.0032
## Epoch 21/50
## 106/106 - 0s - 2ms/step - loss: 0.0046 - val_loss: 0.0031
## Epoch 22/50
## 106/106 - 0s - 2ms/step - loss: 0.0044 - val_loss: 0.0032
## Epoch 23/50
## 106/106 - 0s - 2ms/step - loss: 0.0042 - val_loss: 0.0033
## Epoch 24/50
## 106/106 - 0s - 2ms/step - loss: 0.0041 - val_loss: 0.0031
## Epoch 25/50
## 106/106 - 0s - 2ms/step - loss: 0.0039 - val_loss: 0.0033
## Epoch 26/50
## 106/106 - 0s - 2ms/step - loss: 0.0037 - val_loss: 0.0030
## Epoch 27/50
## 106/106 - 0s - 2ms/step - loss: 0.0035 - val_loss: 0.0032
## Epoch 28/50
## 106/106 - 0s - 2ms/step - loss: 0.0034 - val_loss: 0.0025
## Epoch 29/50
## 106/106 - 0s - 2ms/step - loss: 0.0033 - val_loss: 0.0027
## Epoch 30/50
## 106/106 - 0s - 2ms/step - loss: 0.0032 - val_loss: 0.0029
## Epoch 31/50
## 106/106 - 0s - 3ms/step - loss: 0.0031 - val_loss: 0.0024
## Epoch 32/50
## 106/106 - 0s - 2ms/step - loss: 0.0029 - val_loss: 0.0026
## Epoch 33/50
## 106/106 - 0s - 2ms/step - loss: 0.0029 - val_loss: 0.0026
## Epoch 34/50
## 106/106 - 0s - 2ms/step - loss: 0.0028 - val_loss: 0.0022
## Epoch 35/50
## 106/106 - 0s - 2ms/step - loss: 0.0027 - val_loss: 0.0023
## Epoch 36/50
## 106/106 - 0s - 2ms/step - loss: 0.0026 - val_loss: 0.0025
## Epoch 37/50
## 106/106 - 0s - 2ms/step - loss: 0.0025 - val_loss: 0.0026
## Epoch 38/50
## 106/106 - 0s - 3ms/step - loss: 0.0025 - val_loss: 0.0023
## Epoch 39/50
## 106/106 - 0s - 2ms/step - loss: 0.0024 - val_loss: 0.0023Let’s plot training and validation loss to see how the training went.
plot(history)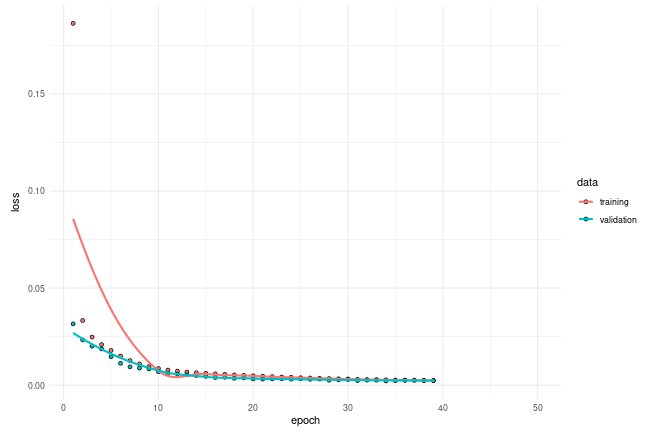
plot of chunk unnamed-chunk-10
Detecting anomalies
We will detect anomalies by determining how well our model can reconstruct the input data.
- Find MAE loss on training samples.
- Find max MAE loss value. This is the worst our model has performed
trying to reconstruct a sample. We will make this the
thresholdfor anomaly detection. - If the reconstruction loss for a sample is greater than this
thresholdvalue then we can infer that the model is seeing a pattern that it isn’t familiar with. We will label this sample as ananomaly.
# Get train MAE loss.
x_train_pred <- model |> predict(x_train)## 118/118 - 0s - 4ms/step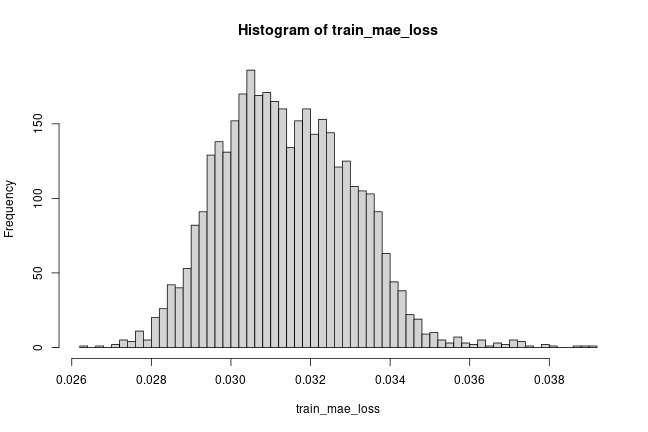
plot of chunk unnamed-chunk-11
# Get reconstruction loss threshold.
threshold <- max(train_mae_loss)
cat("Reconstruction error threshold: ", threshold, "\n")## Reconstruction error threshold: 0.03916234Compare recontruction
Just for fun, let’s see how our model has recontructed the first sample. This is the 288 timesteps from day 1 of our training dataset.
# Checking how the first sequence is learnt
plot(NULL, NULL, ylab = 'Value',
xlim = c(0, TIME_STEPS),
ylim = range(c(x_train[1,,], x_train_pred[1,,])))
lines(x_train[1,,])
lines(x_train_pred[1,,], col = 'red')
legend("topleft", lty = 1,
legend = c("actual", "predicted"),
col = c("black", "red"))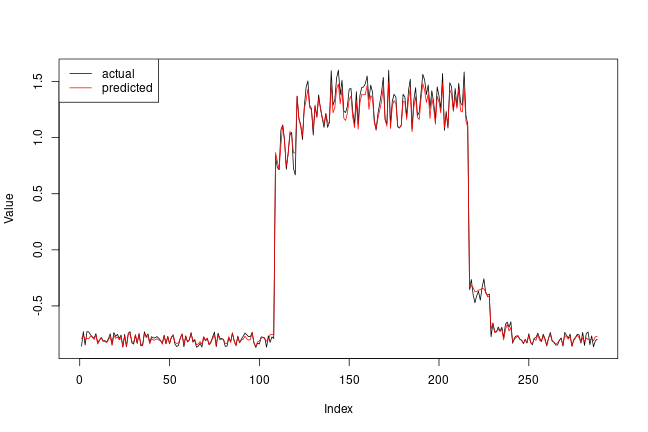
plot of chunk unnamed-chunk-12
Prepare test data
df_test <- df_daily_jumpsup |>
mutate(value =
(value - mean(df_small_noise$value)) /
sd(df_small_noise$value))
df_test |> head()
plot_ts(df_test)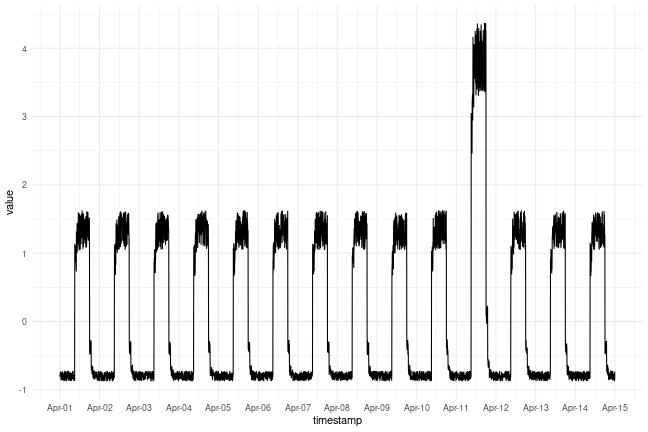
plot of chunk unnamed-chunk-13
# Create sequences from test values.
x_test <- as_dataset(df_test)
# Get test MAE loss.
x_test_pred <- model |> predict(x_test)
test_mae_loss <- apply(abs(x_test_pred - x_test), 1, mean)
hist(test_mae_loss, breaks = 50, xlab = "test MAE loss", ylab = "No of samples")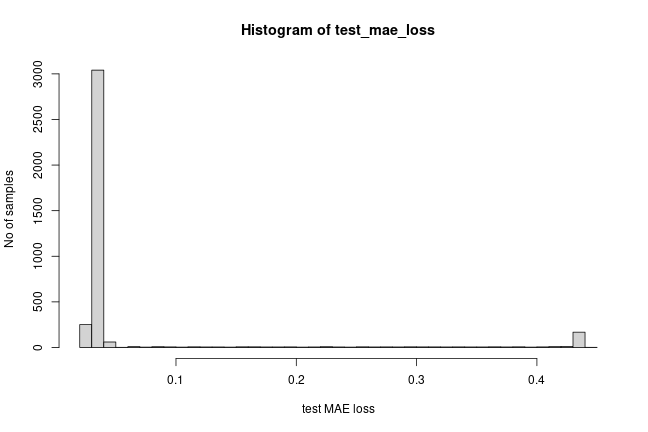
plot of chunk unnamed-chunk-13
# Detect all the samples which are anomalies.
anomalies <- test_mae_loss > threshold
cat("Number of anomaly samples:", sum(anomalies), "\n")
cat("Indices of anomaly samples:", which(anomalies), "\n", fill = TRUE)## # A tibble: 6 × 2
## timestamp value
## <dttm> <dbl>
## 1 2014-04-01 00:00:00 -0.808
## 2 2014-04-01 00:05:00 -0.781
## 3 2014-04-01 00:10:00 -0.801
## 4 2014-04-01 00:15:00 -0.746
## 5 2014-04-01 00:20:00 -0.792
## 6 2014-04-01 00:25:00 -0.802
## 118/118 - 0s - 711us/step
## Number of anomaly samples: 514
## Indices of anomaly samples: 216 217 218 219 220 221 396 398 507 793 794 795
## 797 798 799 861 974 975 1658 1659 1944 1945 1946 1947 1950 2008 2012 2016
## 2018 2020 2022 2024 2026 2028 2036 2038 2040 2042 2044 2045 2046 2048 2050
## 2052 2053 2054 2056 2057 2058 2060 2061 2062 2064 2065 2066 2068 2069 2070
## 2072 2073 2074 2076 2077 2078 2080 2081 2082 2083 2084 2085 2086 2088 2089
## 2090 2092 2093 2094 2096 2097 2098 2100 2101 2102 2104 2105 2106 2108 2110
## 2112 2113 2114 2116 2117 2118 2120 2121 2122 2124 2126 2129 2141 2521 2522
## 2523 2525 2526 2542 2546 2554 2610 2626 2698 2700 2702 2703 2704 2705 2706
## 2707 2708 2709 2710 2711 2712 2713 2714 2715 2716 2717 2718 2719 2720 2721
## 2722 2723 2724 2725 2726 2727 2728 2729 2730 2731 2732 2733 2734 2735 2736
## 2737 2738 2739 2740 2741 2742 2743 2744 2745 2746 2747 2748 2749 2750 2751
## 2752 2753 2754 2755 2756 2757 2758 2759 2760 2761 2762 2763 2764 2765 2766
## 2767 2768 2769 2770 2771 2772 2773 2774 2775 2776 2777 2778 2779 2780 2781
## 2782 2783 2784 2785 2786 2787 2788 2789 2790 2791 2792 2793 2794 2795 2796
## 2797 2798 2799 2800 2801 2802 2803 2804 2805 2806 2807 2808 2809 2810 2811
## 2812 2813 2814 2815 2816 2817 2818 2819 2820 2821 2822 2823 2824 2825 2826
## 2827 2828 2829 2830 2831 2832 2833 2834 2835 2836 2837 2838 2839 2840 2841
## 2842 2843 2844 2845 2846 2847 2848 2849 2850 2851 2852 2853 2854 2855 2856
## 2857 2858 2859 2860 2861 2862 2863 2864 2865 2866 2867 2868 2869 2870 2871
## 2872 2873 2874 2875 2876 2877 2878 2879 2880 2881 2882 2883 2884 2885 2886
## 2887 2888 2889 2890 2891 2892 2893 2894 2895 2896 2897 2898 2899 2900 2901
## 2902 2903 2904 2905 2906 2907 2908 2909 2910 2911 2912 2913 2914 2915 2916
## 2917 2918 2919 2920 2921 2922 2923 2924 2925 2926 2927 2928 2929 2930 2931
## 2932 2933 2934 2935 2936 2937 2938 2939 2940 2941 2942 2943 2944 2945 2946
## 2947 2948 2949 2950 2951 2952 2953 2954 2955 2956 2957 2958 2959 2960 2961
## 2962 2963 2964 2965 2966 2967 2968 2969 2970 2971 2972 2973 2974 2975 2976
## 2977 2978 2979 2980 2981 2982 2983 2984 2985 2986 2987 2988 2989 2990 2991
## 2992 2993 2994 2995 2996 2997 2998 2999 3000 3001 3002 3003 3004 3005 3006
## 3007 3008 3009 3010 3011 3012 3013 3014 3015 3016 3017 3018 3019 3020 3021
## 3022 3023 3024 3025 3026 3027 3028 3029 3030 3031 3032 3033 3034 3035 3036
## 3037 3038 3039 3040 3041 3042 3043 3044 3045 3046 3047 3048 3049 3050 3051
## 3052 3053 3054 3055 3056 3057 3058 3059 3060 3061 3062 3063 3064 3065 3066
## 3067 3068 3069 3070 3071 3072 3073 3074 3075 3076 3077 3078 3079 3080 3081
## 3082 3083 3084 3085 3086 3087 3088 3089 3090 3091 3092 3093 3094 3095 3096
## 3097 3098 3099 3100 3101 3102Plot anomalies
We now know the samples of the data which are anomalies. With this,
we will find the corresponding timestamps from the original
test data. We will be using the following method to do that:
Let’s say time_steps = 3 and we have 10 training values. Our
x_train will look like this:
- 0, 1, 2
- 1, 2, 3
- 2, 3, 4
- 3, 4, 5
- 4, 5, 6
- 5, 6, 7
- 6, 7, 8
- 7, 8, 9
All except the initial and the final time_steps-1 data values, will
appear in time_steps number of samples. So, if we know that
the samples [(3, 4, 5), (4, 5, 6), (5, 6, 7)] are anomalies, we can say
that the data point 5 is an anomaly.
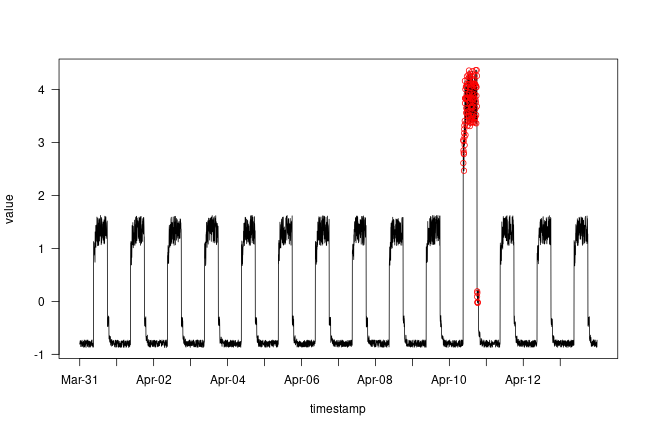
Let’s overlay the anomalies on the original test data plot.
is_anomaly <- test_mae_loss > threshold
is_anomaly <- is_anomaly &
zoo::rollsum(is_anomaly, TIME_STEPS,
align = "right", na.pad = TRUE) >= TIME_STEPS
with(df_test, {
plot(value ~ timestamp, type = 'l', xaxt = 'n', las = 2)
axis.POSIXct(1, at = seq(timestamp[1], tail(timestamp, 1), by = "days"),
format = "%b-%d")
})
with(df_test[which(is_anomaly),], {
points(value ~ timestamp, col = "red")
})
plot of chunk unnamed-chunk-14