Timeseries classification from scratch • keras3

Introduction

This example shows how to do timeseries classification from scratch, starting from raw CSV timeseries files on disk. We demonstrate the workflow on the FordA dataset from the UCR/UEA archive.

Setup

library(keras3)
use_backend("jax")

Load the data: the FordA dataset

Dataset description

The dataset we are using here is called FordA. The data comes from the UCR archive. The dataset contains 3601 training instances and another 1320 testing instances. Each timeseries corresponds to a measurement of engine noise captured by a motor sensor. For this task, the goal is to automatically detect the presence of a specific issue with the engine. The problem is a balanced binary classification task. The full description of this dataset can be found here.

Read the TSV data

We will use the FordA_TRAIN file for training and the FordA_TEST file for testing. The simplicity of this dataset allows us to demonstrate effectively how to use ConvNets for timeseries classification. In this file, the first column corresponds to the label.

get_data <- function(path) {
  if(path |> startsWith("https://"))
    path <- get_file(origin = path)  # cache file locally

  data <- readr::read_tsv(
    path, col_names = FALSE,
    # Each row is: one integer (the label),
    # followed by 500 doubles (the timeseries)
    col_types = paste0("i", strrep("d", 500))
  )

  y <- as.matrix(data[[1]])
  x <- as.matrix(data[,-1])
  dimnames(x) <- dimnames(y) <- NULL

  list(x, y)
}

root_url <- "https://raw.githubusercontent.com/hfawaz/cd-diagram/master/FordA/"
c(x_train, y_train) %<-% get_data(paste0(root_url, "FordA_TRAIN.tsv"))
c(x_test, y_test) %<-% get_data(paste0(root_url, "FordA_TEST.tsv"))

str(keras3:::named_list(
  x_train, y_train,
  x_test, y_test
))

## List of 4
##  $ x_train: num [1:3601, 1:500] -0.797 0.805 0.728 -0.234 -0.171 ...
##  $ y_train: int [1:3601, 1] -1 1 -1 -1 -1 1 1 1 1 1 ...
##  $ x_test : num [1:1320, 1:500] -0.14 0.334 0.717 1.24 -1.159 ...
##  $ y_test : int [1:1320, 1] -1 -1 -1 1 -1 1 -1 -1 1 1 ...

Visualize the data

Here we visualize one timeseries example for each class in the dataset.

plot(NULL, main = "Timeseries Data",
     xlab = "Timepoints",  ylab = "Values",
     xlim = c(1, ncol(x_test)),
     ylim = range(x_test))
grid()
lines(x_test[match(-1, y_test), ], col = "blue")
lines(x_test[match( 1, y_test), ], col = "red")
legend("topright", legend=c("label -1", "label 1"), col=c("blue", "red"), lty=1)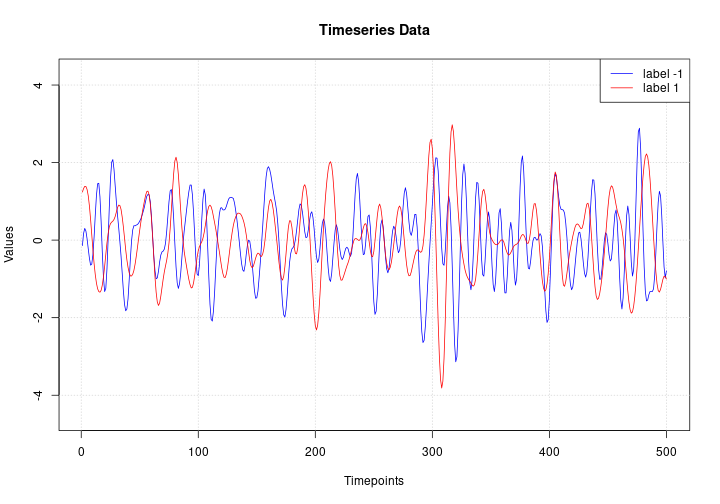

Plot of Example Timeseries Data

Standardize the data

Our timeseries are already in a single length (500). However, their values are usually in various ranges. This is not ideal for a neural network; in general we should seek to make the input values normalized. For this specific dataset, the data is already z-normalized: each timeseries sample has a mean equal to zero and a standard deviation equal to one. This type of normalization is very common for timeseries classification problems, see Bagnall et al. (2016).

Note that the timeseries data used here are univariate, meaning we only have one channel per timeseries example. We will therefore transform the timeseries into a multivariate one with one channel using a simple reshaping via numpy. This will allow us to construct a model that is easily applicable to multivariate time series.

dim(x_train) <- c(dim(x_train), 1)
dim(x_test) <- c(dim(x_test), 1)

Finally, in order to use sparse_categorical_crossentropy, we will have to count the number of classes beforehand.

num_classes <- length(unique(y_train))

Now we shuffle the training set because we will be using the validation_split option later when training.

c(x_train, y_train) %<-% listarrays::shuffle_rows(x_train, y_train)
# idx <- sample.int(nrow(x_train))
# x_train %<>% .[idx,, ,drop = FALSE]
# y_train %<>% .[idx,  ,drop = FALSE]

Standardize the labels to positive integers. The expected labels will then be 0 and 1.

y_train[y_train == -1L] <- 0L
y_test[y_test == -1L] <- 0L

Build a model

We build a Fully Convolutional Neural Network originally proposed in this paper. The implementation is based on the TF 2 version provided here. The following hyperparameters (kernel_size, filters, the usage of BatchNorm) were found via random search using KerasTuner.

make_model <- function(input_shape) {
  inputs <- keras_input(input_shape)

  outputs <- inputs |>
    # conv1
    layer_conv_1d(filters = 64, kernel_size = 3, padding = "same") |>
    layer_batch_normalization() |>
    layer_activation_relu() |>
    # conv2
    layer_conv_1d(filters = 64, kernel_size = 3, padding = "same") |>
    layer_batch_normalization() |>
    layer_activation_relu() |>
    # conv3
    layer_conv_1d(filters = 64, kernel_size = 3, padding = "same") |>
    layer_batch_normalization() |>
    layer_activation_relu() |>
    # pooling
    layer_global_average_pooling_1d() |>
    # final output
    layer_dense(num_classes, activation = "softmax")

  keras_model(inputs, outputs)
}

model <- make_model(input_shape = dim(x_train)[-1])

model

## Model: "functional"
## ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━┓
## ┃ Layer (type)                ┃ Output Shape          ┃    Param # ┃ Trai… ┃
## ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━┩
## │ input_layer (InputLayer)    │ (None, 500, 1)        │          0 │   -   │
## ├─────────────────────────────┼───────────────────────┼────────────┼───────┤
## │ conv1d (Conv1D)             │ (None, 500, 64)       │        256 │   Y   │
## ├─────────────────────────────┼───────────────────────┼────────────┼───────┤
## │ batch_normalization         │ (None, 500, 64)       │        256 │   Y   │
## │ (BatchNormalization)        │                       │            │       │
## ├─────────────────────────────┼───────────────────────┼────────────┼───────┤
## │ re_lu (ReLU)                │ (None, 500, 64)       │          0 │   -   │
## ├─────────────────────────────┼───────────────────────┼────────────┼───────┤
## │ conv1d_1 (Conv1D)           │ (None, 500, 64)       │     12,352 │   Y   │
## ├─────────────────────────────┼───────────────────────┼────────────┼───────┤
## │ batch_normalization_1       │ (None, 500, 64)       │        256 │   Y   │
## │ (BatchNormalization)        │                       │            │       │
## ├─────────────────────────────┼───────────────────────┼────────────┼───────┤
## │ re_lu_1 (ReLU)              │ (None, 500, 64)       │          0 │   -   │
## ├─────────────────────────────┼───────────────────────┼────────────┼───────┤
## │ conv1d_2 (Conv1D)           │ (None, 500, 64)       │     12,352 │   Y   │
## ├─────────────────────────────┼───────────────────────┼────────────┼───────┤
## │ batch_normalization_2       │ (None, 500, 64)       │        256 │   Y   │
## │ (BatchNormalization)        │                       │            │       │
## ├─────────────────────────────┼───────────────────────┼────────────┼───────┤
## │ re_lu_2 (ReLU)              │ (None, 500, 64)       │          0 │   -   │
## ├─────────────────────────────┼───────────────────────┼────────────┼───────┤
## │ global_average_pooling1d    │ (None, 64)            │          0 │   -   │
## │ (GlobalAveragePooling1D)    │                       │            │       │
## ├─────────────────────────────┼───────────────────────┼────────────┼───────┤
## │ dense (Dense)               │ (None, 2)             │        130 │   Y   │
## └─────────────────────────────┴───────────────────────┴────────────┴───────┘
##  Total params: 25,858 (101.01 KB)
##  Trainable params: 25,474 (99.51 KB)
##  Non-trainable params: 384 (1.50 KB)

plot(model, show_shapes = TRUE)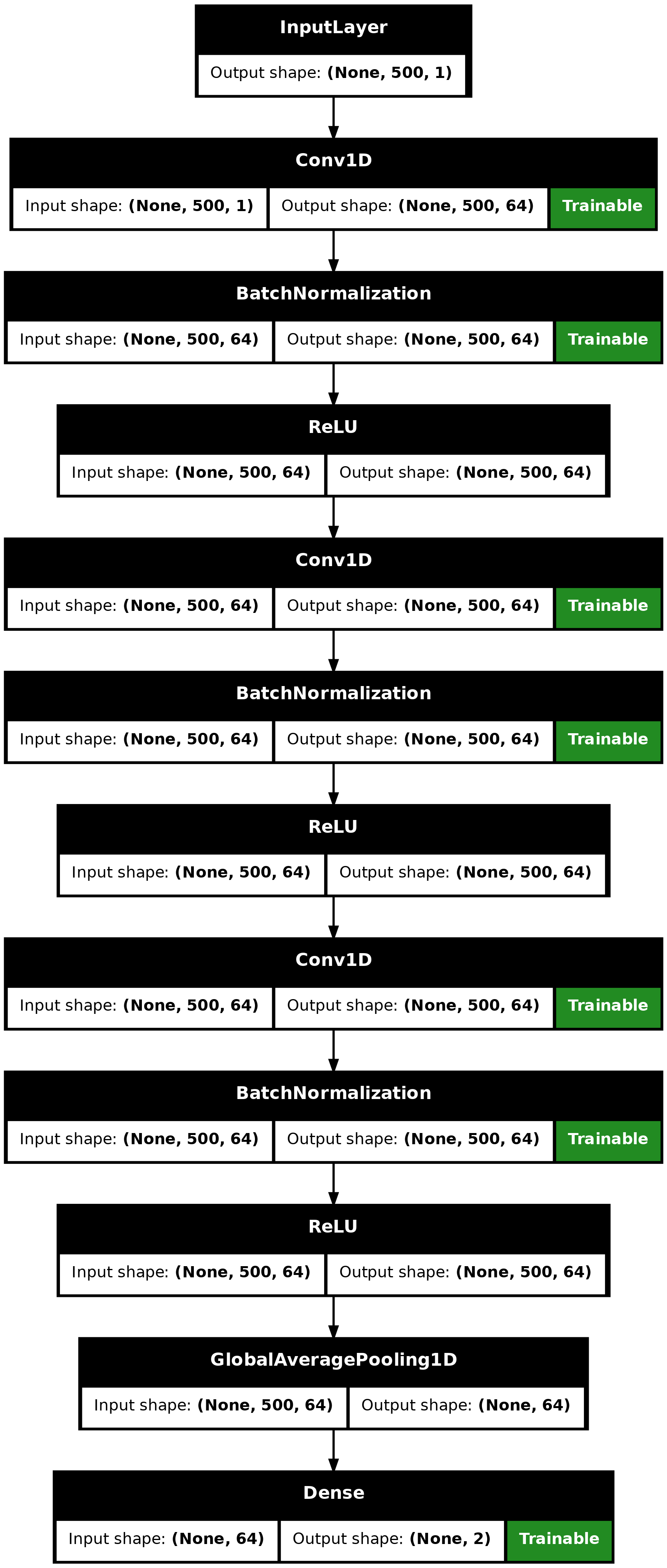

plot of chunk unnamed-chunk-9

Train the model

epochs <- 500
batch_size <- 32

callbacks <- c(
  callback_model_checkpoint(
    "best_model.keras", save_best_only = TRUE,
    monitor = "val_loss"
  ),
  callback_reduce_lr_on_plateau(
    monitor = "val_loss", factor = 0.5,
    patience = 20, min_lr = 0.0001
  ),
  callback_early_stopping(
    monitor = "val_loss", patience = 50,
    verbose = 1
  )
)


model |> compile(
  optimizer = "adam",
  loss = "sparse_categorical_crossentropy",
  metrics = "sparse_categorical_accuracy"
)

history <- model |> fit(
  x_train, y_train,
  batch_size = batch_size,
  epochs = epochs,
  callbacks = callbacks,
  validation_split = 0.2
)

## Epoch 1/500
## 90/90 - 3s - 33ms/step - loss: 0.5311 - sparse_categorical_accuracy: 0.7160 - val_loss: 0.7862 - val_sparse_categorical_accuracy: 0.4896 - learning_rate: 0.0010
## Epoch 2/500
## 90/90 - 0s - 2ms/step - loss: 0.4772 - sparse_categorical_accuracy: 0.7663 - val_loss: 0.8646 - val_sparse_categorical_accuracy: 0.4896 - learning_rate: 0.0010
## Epoch 3/500
## 90/90 - 0s - 2ms/step - loss: 0.4647 - sparse_categorical_accuracy: 0.7622 - val_loss: 0.9484 - val_sparse_categorical_accuracy: 0.4896 - learning_rate: 0.0010
## Epoch 4/500
## 90/90 - 0s - 2ms/step - loss: 0.4082 - sparse_categorical_accuracy: 0.7997 - val_loss: 0.6787 - val_sparse_categorical_accuracy: 0.5062 - learning_rate: 0.0010
## Epoch 5/500
## 90/90 - 0s - 2ms/step - loss: 0.4205 - sparse_categorical_accuracy: 0.7806 - val_loss: 0.5032 - val_sparse_categorical_accuracy: 0.6921 - learning_rate: 0.0010
## Epoch 6/500
## 90/90 - 0s - 2ms/step - loss: 0.3966 - sparse_categorical_accuracy: 0.8069 - val_loss: 0.4293 - val_sparse_categorical_accuracy: 0.7725 - learning_rate: 0.0010
## Epoch 7/500
## 90/90 - 0s - 2ms/step - loss: 0.3878 - sparse_categorical_accuracy: 0.8132 - val_loss: 0.6504 - val_sparse_categorical_accuracy: 0.6893 - learning_rate: 0.0010
## Epoch 8/500
## 90/90 - 0s - 2ms/step - loss: 0.3764 - sparse_categorical_accuracy: 0.8163 - val_loss: 0.3956 - val_sparse_categorical_accuracy: 0.7920 - learning_rate: 0.0010
## Epoch 9/500
## 90/90 - 0s - 2ms/step - loss: 0.3767 - sparse_categorical_accuracy: 0.8219 - val_loss: 0.7247 - val_sparse_categorical_accuracy: 0.6325 - learning_rate: 0.0010
## Epoch 10/500
## 90/90 - 0s - 2ms/step - loss: 0.3629 - sparse_categorical_accuracy: 0.8281 - val_loss: 0.3612 - val_sparse_categorical_accuracy: 0.8391 - learning_rate: 0.0010
## Epoch 11/500
## 90/90 - 0s - 2ms/step - loss: 0.3561 - sparse_categorical_accuracy: 0.8333 - val_loss: 0.4864 - val_sparse_categorical_accuracy: 0.7545 - learning_rate: 0.0010
## Epoch 12/500
## 90/90 - 0s - 2ms/step - loss: 0.3467 - sparse_categorical_accuracy: 0.8403 - val_loss: 0.4411 - val_sparse_categorical_accuracy: 0.7767 - learning_rate: 0.0010
## Epoch 13/500
## 90/90 - 0s - 2ms/step - loss: 0.3287 - sparse_categorical_accuracy: 0.8608 - val_loss: 0.3528 - val_sparse_categorical_accuracy: 0.8308 - learning_rate: 0.0010
## Epoch 14/500
## 90/90 - 0s - 2ms/step - loss: 0.3310 - sparse_categorical_accuracy: 0.8517 - val_loss: 1.2018 - val_sparse_categorical_accuracy: 0.7060 - learning_rate: 0.0010
## Epoch 15/500
## 90/90 - 0s - 2ms/step - loss: 0.3293 - sparse_categorical_accuracy: 0.8528 - val_loss: 0.7427 - val_sparse_categorical_accuracy: 0.6186 - learning_rate: 0.0010
## Epoch 16/500
## 90/90 - 0s - 2ms/step - loss: 0.3302 - sparse_categorical_accuracy: 0.8583 - val_loss: 0.5381 - val_sparse_categorical_accuracy: 0.7143 - learning_rate: 0.0010
## Epoch 17/500
## 90/90 - 0s - 2ms/step - loss: 0.3097 - sparse_categorical_accuracy: 0.8646 - val_loss: 0.4011 - val_sparse_categorical_accuracy: 0.7933 - learning_rate: 0.0010
## Epoch 18/500
## 90/90 - 0s - 2ms/step - loss: 0.3060 - sparse_categorical_accuracy: 0.8667 - val_loss: 0.7731 - val_sparse_categorical_accuracy: 0.6255 - learning_rate: 0.0010
## Epoch 19/500
## 90/90 - 0s - 2ms/step - loss: 0.3001 - sparse_categorical_accuracy: 0.8736 - val_loss: 1.2595 - val_sparse_categorical_accuracy: 0.5506 - learning_rate: 0.0010
## Epoch 20/500
## 90/90 - 0s - 1ms/step - loss: 0.3000 - sparse_categorical_accuracy: 0.8757 - val_loss: 0.6590 - val_sparse_categorical_accuracy: 0.6657 - learning_rate: 0.0010
## Epoch 21/500
## 90/90 - 0s - 2ms/step - loss: 0.2828 - sparse_categorical_accuracy: 0.8799 - val_loss: 0.2971 - val_sparse_categorical_accuracy: 0.8669 - learning_rate: 0.0010
## Epoch 22/500
## 90/90 - 0s - 2ms/step - loss: 0.2946 - sparse_categorical_accuracy: 0.8771 - val_loss: 0.7545 - val_sparse_categorical_accuracy: 0.7268 - learning_rate: 0.0010
## Epoch 23/500
## 90/90 - 0s - 2ms/step - loss: 0.2751 - sparse_categorical_accuracy: 0.8889 - val_loss: 0.7695 - val_sparse_categorical_accuracy: 0.7101 - learning_rate: 0.0010
## Epoch 24/500
## 90/90 - 0s - 1ms/step - loss: 0.2750 - sparse_categorical_accuracy: 0.8847 - val_loss: 0.3635 - val_sparse_categorical_accuracy: 0.8419 - learning_rate: 0.0010
## Epoch 25/500
## 90/90 - 0s - 2ms/step - loss: 0.2672 - sparse_categorical_accuracy: 0.8899 - val_loss: 0.2758 - val_sparse_categorical_accuracy: 0.8821 - learning_rate: 0.0010
## Epoch 26/500
## 90/90 - 0s - 2ms/step - loss: 0.3037 - sparse_categorical_accuracy: 0.8649 - val_loss: 0.3801 - val_sparse_categorical_accuracy: 0.8155 - learning_rate: 0.0010
## Epoch 27/500
## 90/90 - 0s - 2ms/step - loss: 0.2614 - sparse_categorical_accuracy: 0.8986 - val_loss: 0.2762 - val_sparse_categorical_accuracy: 0.8863 - learning_rate: 0.0010
## Epoch 28/500
## 90/90 - 0s - 2ms/step - loss: 0.2835 - sparse_categorical_accuracy: 0.8795 - val_loss: 1.2893 - val_sparse_categorical_accuracy: 0.6990 - learning_rate: 0.0010
## Epoch 29/500
## 90/90 - 0s - 2ms/step - loss: 0.2684 - sparse_categorical_accuracy: 0.8802 - val_loss: 0.4549 - val_sparse_categorical_accuracy: 0.7822 - learning_rate: 0.0010
## Epoch 30/500
## 90/90 - 0s - 2ms/step - loss: 0.2590 - sparse_categorical_accuracy: 0.8910 - val_loss: 0.4562 - val_sparse_categorical_accuracy: 0.7933 - learning_rate: 0.0010
## Epoch 31/500
## 90/90 - 0s - 1ms/step - loss: 0.2600 - sparse_categorical_accuracy: 0.8990 - val_loss: 0.3994 - val_sparse_categorical_accuracy: 0.8044 - learning_rate: 0.0010
## Epoch 32/500
## 90/90 - 0s - 1ms/step - loss: 0.2559 - sparse_categorical_accuracy: 0.8944 - val_loss: 0.3455 - val_sparse_categorical_accuracy: 0.8044 - learning_rate: 0.0010
## Epoch 33/500
## 90/90 - 0s - 2ms/step - loss: 0.2447 - sparse_categorical_accuracy: 0.9010 - val_loss: 0.3526 - val_sparse_categorical_accuracy: 0.8502 - learning_rate: 0.0010
## Epoch 34/500
## 90/90 - 0s - 2ms/step - loss: 0.2353 - sparse_categorical_accuracy: 0.9042 - val_loss: 0.6348 - val_sparse_categorical_accuracy: 0.7018 - learning_rate: 0.0010
## Epoch 35/500
## 90/90 - 0s - 2ms/step - loss: 0.2598 - sparse_categorical_accuracy: 0.8924 - val_loss: 0.2751 - val_sparse_categorical_accuracy: 0.8793 - learning_rate: 0.0010
## Epoch 36/500
## 90/90 - 0s - 1ms/step - loss: 0.2424 - sparse_categorical_accuracy: 0.9010 - val_loss: 0.3424 - val_sparse_categorical_accuracy: 0.8183 - learning_rate: 0.0010
## Epoch 37/500
## 90/90 - 0s - 1ms/step - loss: 0.2404 - sparse_categorical_accuracy: 0.9007 - val_loss: 0.3547 - val_sparse_categorical_accuracy: 0.8239 - learning_rate: 0.0010
## Epoch 38/500
## 90/90 - 0s - 2ms/step - loss: 0.2436 - sparse_categorical_accuracy: 0.9038 - val_loss: 0.9114 - val_sparse_categorical_accuracy: 0.7282 - learning_rate: 0.0010
## Epoch 39/500
## 90/90 - 0s - 2ms/step - loss: 0.2381 - sparse_categorical_accuracy: 0.9014 - val_loss: 1.4388 - val_sparse_categorical_accuracy: 0.5548 - learning_rate: 0.0010
## Epoch 40/500
## 90/90 - 0s - 1ms/step - loss: 0.2312 - sparse_categorical_accuracy: 0.9010 - val_loss: 1.2421 - val_sparse_categorical_accuracy: 0.5742 - learning_rate: 0.0010
## Epoch 41/500
## 90/90 - 0s - 2ms/step - loss: 0.2255 - sparse_categorical_accuracy: 0.9111 - val_loss: 0.4272 - val_sparse_categorical_accuracy: 0.8086 - learning_rate: 0.0010
## Epoch 42/500
## 90/90 - 0s - 2ms/step - loss: 0.2144 - sparse_categorical_accuracy: 0.9208 - val_loss: 0.4859 - val_sparse_categorical_accuracy: 0.7975 - learning_rate: 0.0010
## Epoch 43/500
## 90/90 - 0s - 2ms/step - loss: 0.2217 - sparse_categorical_accuracy: 0.9115 - val_loss: 0.3361 - val_sparse_categorical_accuracy: 0.8530 - learning_rate: 0.0010
## Epoch 44/500
## 90/90 - 0s - 2ms/step - loss: 0.2185 - sparse_categorical_accuracy: 0.9139 - val_loss: 0.3998 - val_sparse_categorical_accuracy: 0.8058 - learning_rate: 0.0010
## Epoch 45/500
## 90/90 - 0s - 2ms/step - loss: 0.2230 - sparse_categorical_accuracy: 0.9115 - val_loss: 0.4232 - val_sparse_categorical_accuracy: 0.8114 - learning_rate: 0.0010
## Epoch 46/500
## 90/90 - 0s - 2ms/step - loss: 0.2176 - sparse_categorical_accuracy: 0.9153 - val_loss: 0.3560 - val_sparse_categorical_accuracy: 0.8183 - learning_rate: 0.0010
## Epoch 47/500
## 90/90 - 0s - 2ms/step - loss: 0.1980 - sparse_categorical_accuracy: 0.9274 - val_loss: 0.3046 - val_sparse_categorical_accuracy: 0.8696 - learning_rate: 0.0010
## Epoch 48/500
## 90/90 - 0s - 2ms/step - loss: 0.1975 - sparse_categorical_accuracy: 0.9205 - val_loss: 0.4666 - val_sparse_categorical_accuracy: 0.7822 - learning_rate: 0.0010
## Epoch 49/500
## 90/90 - 0s - 2ms/step - loss: 0.1879 - sparse_categorical_accuracy: 0.9247 - val_loss: 0.2679 - val_sparse_categorical_accuracy: 0.8766 - learning_rate: 0.0010
## Epoch 50/500
## 90/90 - 0s - 2ms/step - loss: 0.2166 - sparse_categorical_accuracy: 0.9142 - val_loss: 0.3123 - val_sparse_categorical_accuracy: 0.8585 - learning_rate: 0.0010
## Epoch 51/500
## 90/90 - 0s - 2ms/step - loss: 0.1946 - sparse_categorical_accuracy: 0.9264 - val_loss: 0.2322 - val_sparse_categorical_accuracy: 0.8932 - learning_rate: 0.0010
## Epoch 52/500
## 90/90 - 0s - 2ms/step - loss: 0.1779 - sparse_categorical_accuracy: 0.9347 - val_loss: 0.2967 - val_sparse_categorical_accuracy: 0.8766 - learning_rate: 0.0010
## Epoch 53/500
## 90/90 - 0s - 2ms/step - loss: 0.1720 - sparse_categorical_accuracy: 0.9351 - val_loss: 0.3407 - val_sparse_categorical_accuracy: 0.8405 - learning_rate: 0.0010
## Epoch 54/500
## 90/90 - 0s - 2ms/step - loss: 0.1623 - sparse_categorical_accuracy: 0.9431 - val_loss: 0.2135 - val_sparse_categorical_accuracy: 0.8988 - learning_rate: 0.0010
## Epoch 55/500
## 90/90 - 0s - 2ms/step - loss: 0.1629 - sparse_categorical_accuracy: 0.9431 - val_loss: 0.5253 - val_sparse_categorical_accuracy: 0.7850 - learning_rate: 0.0010
## Epoch 56/500
## 90/90 - 0s - 2ms/step - loss: 0.1507 - sparse_categorical_accuracy: 0.9510 - val_loss: 0.3022 - val_sparse_categorical_accuracy: 0.8904 - learning_rate: 0.0010
## Epoch 57/500
## 90/90 - 0s - 2ms/step - loss: 0.1460 - sparse_categorical_accuracy: 0.9524 - val_loss: 0.2083 - val_sparse_categorical_accuracy: 0.9182 - learning_rate: 0.0010
## Epoch 58/500
## 90/90 - 0s - 2ms/step - loss: 0.1354 - sparse_categorical_accuracy: 0.9569 - val_loss: 0.2619 - val_sparse_categorical_accuracy: 0.8724 - learning_rate: 0.0010
## Epoch 59/500
## 90/90 - 0s - 2ms/step - loss: 0.1410 - sparse_categorical_accuracy: 0.9497 - val_loss: 0.1803 - val_sparse_categorical_accuracy: 0.9293 - learning_rate: 0.0010
## Epoch 60/500
## 90/90 - 0s - 2ms/step - loss: 0.1318 - sparse_categorical_accuracy: 0.9566 - val_loss: 0.1931 - val_sparse_categorical_accuracy: 0.9071 - learning_rate: 0.0010
## Epoch 61/500
## 90/90 - 0s - 1ms/step - loss: 0.1277 - sparse_categorical_accuracy: 0.9587 - val_loss: 3.3490 - val_sparse_categorical_accuracy: 0.6755 - learning_rate: 0.0010
## Epoch 62/500
## 90/90 - 0s - 2ms/step - loss: 0.1383 - sparse_categorical_accuracy: 0.9569 - val_loss: 0.2036 - val_sparse_categorical_accuracy: 0.9057 - learning_rate: 0.0010
## Epoch 63/500
## 90/90 - 0s - 1ms/step - loss: 0.1339 - sparse_categorical_accuracy: 0.9531 - val_loss: 0.3220 - val_sparse_categorical_accuracy: 0.8627 - learning_rate: 0.0010
## Epoch 64/500
## 90/90 - 0s - 2ms/step - loss: 0.1310 - sparse_categorical_accuracy: 0.9569 - val_loss: 0.2703 - val_sparse_categorical_accuracy: 0.8793 - learning_rate: 0.0010
## Epoch 65/500
## 90/90 - 0s - 2ms/step - loss: 0.1240 - sparse_categorical_accuracy: 0.9594 - val_loss: 0.2623 - val_sparse_categorical_accuracy: 0.8932 - learning_rate: 0.0010
## Epoch 66/500
## 90/90 - 0s - 1ms/step - loss: 0.1110 - sparse_categorical_accuracy: 0.9653 - val_loss: 0.2723 - val_sparse_categorical_accuracy: 0.8918 - learning_rate: 0.0010
## Epoch 67/500
## 90/90 - 0s - 2ms/step - loss: 0.1322 - sparse_categorical_accuracy: 0.9552 - val_loss: 1.6294 - val_sparse_categorical_accuracy: 0.6491 - learning_rate: 0.0010
## Epoch 68/500
## 90/90 - 0s - 1ms/step - loss: 0.1260 - sparse_categorical_accuracy: 0.9594 - val_loss: 0.4498 - val_sparse_categorical_accuracy: 0.7989 - learning_rate: 0.0010
## Epoch 69/500
## 90/90 - 0s - 1ms/step - loss: 0.1235 - sparse_categorical_accuracy: 0.9604 - val_loss: 0.9340 - val_sparse_categorical_accuracy: 0.7282 - learning_rate: 0.0010
## Epoch 70/500
## 90/90 - 0s - 1ms/step - loss: 0.1145 - sparse_categorical_accuracy: 0.9646 - val_loss: 0.2487 - val_sparse_categorical_accuracy: 0.9043 - learning_rate: 0.0010
## Epoch 71/500
## 90/90 - 0s - 1ms/step - loss: 0.1160 - sparse_categorical_accuracy: 0.9625 - val_loss: 0.3497 - val_sparse_categorical_accuracy: 0.8599 - learning_rate: 0.0010
## Epoch 72/500
## 90/90 - 0s - 2ms/step - loss: 0.1148 - sparse_categorical_accuracy: 0.9632 - val_loss: 0.1281 - val_sparse_categorical_accuracy: 0.9515 - learning_rate: 0.0010
## Epoch 73/500
## 90/90 - 0s - 2ms/step - loss: 0.1101 - sparse_categorical_accuracy: 0.9642 - val_loss: 0.2499 - val_sparse_categorical_accuracy: 0.9043 - learning_rate: 0.0010
## Epoch 74/500
## 90/90 - 0s - 2ms/step - loss: 0.1049 - sparse_categorical_accuracy: 0.9649 - val_loss: 0.1516 - val_sparse_categorical_accuracy: 0.9390 - learning_rate: 0.0010
## Epoch 75/500
## 90/90 - 0s - 2ms/step - loss: 0.1196 - sparse_categorical_accuracy: 0.9583 - val_loss: 0.6438 - val_sparse_categorical_accuracy: 0.7032 - learning_rate: 0.0010
## Epoch 76/500
## 90/90 - 0s - 2ms/step - loss: 0.1135 - sparse_categorical_accuracy: 0.9632 - val_loss: 0.1870 - val_sparse_categorical_accuracy: 0.9196 - learning_rate: 0.0010
## Epoch 77/500
## 90/90 - 0s - 1ms/step - loss: 0.1079 - sparse_categorical_accuracy: 0.9615 - val_loss: 0.1711 - val_sparse_categorical_accuracy: 0.9293 - learning_rate: 0.0010
## Epoch 78/500
## 90/90 - 0s - 1ms/step - loss: 0.1010 - sparse_categorical_accuracy: 0.9688 - val_loss: 0.1364 - val_sparse_categorical_accuracy: 0.9390 - learning_rate: 0.0010
## Epoch 79/500
## 90/90 - 0s - 1ms/step - loss: 0.1029 - sparse_categorical_accuracy: 0.9677 - val_loss: 1.2676 - val_sparse_categorical_accuracy: 0.7295 - learning_rate: 0.0010
## Epoch 80/500
## 90/90 - 0s - 1ms/step - loss: 0.1024 - sparse_categorical_accuracy: 0.9691 - val_loss: 0.1891 - val_sparse_categorical_accuracy: 0.9320 - learning_rate: 0.0010
## Epoch 81/500
## 90/90 - 0s - 1ms/step - loss: 0.1134 - sparse_categorical_accuracy: 0.9642 - val_loss: 0.2274 - val_sparse_categorical_accuracy: 0.9098 - learning_rate: 0.0010
## Epoch 82/500
## 90/90 - 0s - 1ms/step - loss: 0.1041 - sparse_categorical_accuracy: 0.9684 - val_loss: 1.1301 - val_sparse_categorical_accuracy: 0.7212 - learning_rate: 0.0010
## Epoch 83/500
## 90/90 - 0s - 1ms/step - loss: 0.1058 - sparse_categorical_accuracy: 0.9625 - val_loss: 0.1301 - val_sparse_categorical_accuracy: 0.9431 - learning_rate: 0.0010
## Epoch 84/500
## 90/90 - 0s - 1ms/step - loss: 0.1047 - sparse_categorical_accuracy: 0.9646 - val_loss: 0.1451 - val_sparse_categorical_accuracy: 0.9501 - learning_rate: 0.0010
## Epoch 85/500
## 90/90 - 0s - 1ms/step - loss: 0.1061 - sparse_categorical_accuracy: 0.9663 - val_loss: 0.1899 - val_sparse_categorical_accuracy: 0.9196 - learning_rate: 0.0010
## Epoch 86/500
## 90/90 - 0s - 2ms/step - loss: 0.1020 - sparse_categorical_accuracy: 0.9646 - val_loss: 0.1263 - val_sparse_categorical_accuracy: 0.9459 - learning_rate: 0.0010
## Epoch 87/500
## 90/90 - 0s - 2ms/step - loss: 0.1071 - sparse_categorical_accuracy: 0.9635 - val_loss: 0.1395 - val_sparse_categorical_accuracy: 0.9501 - learning_rate: 0.0010
## Epoch 88/500
## 90/90 - 0s - 2ms/step - loss: 0.0991 - sparse_categorical_accuracy: 0.9688 - val_loss: 0.1515 - val_sparse_categorical_accuracy: 0.9334 - learning_rate: 0.0010
## Epoch 89/500
## 90/90 - 0s - 2ms/step - loss: 0.1059 - sparse_categorical_accuracy: 0.9618 - val_loss: 0.1525 - val_sparse_categorical_accuracy: 0.9473 - learning_rate: 0.0010
## Epoch 90/500
## 90/90 - 0s - 2ms/step - loss: 0.1062 - sparse_categorical_accuracy: 0.9660 - val_loss: 0.1628 - val_sparse_categorical_accuracy: 0.9251 - learning_rate: 0.0010
## Epoch 91/500
## 90/90 - 0s - 2ms/step - loss: 0.1161 - sparse_categorical_accuracy: 0.9608 - val_loss: 0.6074 - val_sparse_categorical_accuracy: 0.7587 - learning_rate: 0.0010
## Epoch 92/500
## 90/90 - 0s - 1ms/step - loss: 0.1047 - sparse_categorical_accuracy: 0.9660 - val_loss: 1.3042 - val_sparse_categorical_accuracy: 0.7115 - learning_rate: 0.0010
## Epoch 93/500
## 90/90 - 0s - 1ms/step - loss: 0.0974 - sparse_categorical_accuracy: 0.9681 - val_loss: 2.3294 - val_sparse_categorical_accuracy: 0.6865 - learning_rate: 0.0010
## Epoch 94/500
## 90/90 - 0s - 2ms/step - loss: 0.0987 - sparse_categorical_accuracy: 0.9677 - val_loss: 2.4967 - val_sparse_categorical_accuracy: 0.6588 - learning_rate: 0.0010
## Epoch 95/500
## 90/90 - 0s - 2ms/step - loss: 0.0949 - sparse_categorical_accuracy: 0.9694 - val_loss: 2.4758 - val_sparse_categorical_accuracy: 0.6061 - learning_rate: 0.0010
## Epoch 96/500
## 90/90 - 0s - 1ms/step - loss: 0.1081 - sparse_categorical_accuracy: 0.9597 - val_loss: 1.3334 - val_sparse_categorical_accuracy: 0.6699 - learning_rate: 0.0010
## Epoch 97/500
## 90/90 - 0s - 2ms/step - loss: 0.1014 - sparse_categorical_accuracy: 0.9646 - val_loss: 0.2643 - val_sparse_categorical_accuracy: 0.9057 - learning_rate: 0.0010
## Epoch 98/500
## 90/90 - 0s - 2ms/step - loss: 0.0939 - sparse_categorical_accuracy: 0.9694 - val_loss: 0.2298 - val_sparse_categorical_accuracy: 0.9071 - learning_rate: 0.0010
## Epoch 99/500
## 90/90 - 0s - 1ms/step - loss: 0.0973 - sparse_categorical_accuracy: 0.9649 - val_loss: 0.3342 - val_sparse_categorical_accuracy: 0.8863 - learning_rate: 0.0010
## Epoch 100/500
## 90/90 - 0s - 1ms/step - loss: 0.0953 - sparse_categorical_accuracy: 0.9712 - val_loss: 0.3691 - val_sparse_categorical_accuracy: 0.8710 - learning_rate: 0.0010
## Epoch 101/500
## 90/90 - 0s - 1ms/step - loss: 0.0886 - sparse_categorical_accuracy: 0.9705 - val_loss: 0.4206 - val_sparse_categorical_accuracy: 0.8391 - learning_rate: 0.0010
## Epoch 102/500
## 90/90 - 0s - 1ms/step - loss: 0.1112 - sparse_categorical_accuracy: 0.9615 - val_loss: 0.2451 - val_sparse_categorical_accuracy: 0.9085 - learning_rate: 0.0010
## Epoch 103/500
## 90/90 - 0s - 1ms/step - loss: 0.0940 - sparse_categorical_accuracy: 0.9698 - val_loss: 0.3129 - val_sparse_categorical_accuracy: 0.8738 - learning_rate: 0.0010
## Epoch 104/500
## 90/90 - 0s - 2ms/step - loss: 0.1024 - sparse_categorical_accuracy: 0.9625 - val_loss: 0.6503 - val_sparse_categorical_accuracy: 0.7920 - learning_rate: 0.0010
## Epoch 105/500
## 90/90 - 0s - 2ms/step - loss: 0.1001 - sparse_categorical_accuracy: 0.9660 - val_loss: 0.5994 - val_sparse_categorical_accuracy: 0.7933 - learning_rate: 0.0010
## Epoch 106/500
## 90/90 - 0s - 2ms/step - loss: 0.0903 - sparse_categorical_accuracy: 0.9708 - val_loss: 1.3070 - val_sparse_categorical_accuracy: 0.6477 - learning_rate: 0.0010
## Epoch 107/500
## 90/90 - 0s - 2ms/step - loss: 0.0845 - sparse_categorical_accuracy: 0.9722 - val_loss: 0.1213 - val_sparse_categorical_accuracy: 0.9584 - learning_rate: 5.0000e-04
## Epoch 108/500
## 90/90 - 0s - 2ms/step - loss: 0.0778 - sparse_categorical_accuracy: 0.9753 - val_loss: 0.1091 - val_sparse_categorical_accuracy: 0.9570 - learning_rate: 5.0000e-04
## Epoch 109/500
## 90/90 - 0s - 1ms/step - loss: 0.0844 - sparse_categorical_accuracy: 0.9715 - val_loss: 0.4146 - val_sparse_categorical_accuracy: 0.8655 - learning_rate: 5.0000e-04
## Epoch 110/500
## 90/90 - 0s - 2ms/step - loss: 0.0854 - sparse_categorical_accuracy: 0.9719 - val_loss: 0.1178 - val_sparse_categorical_accuracy: 0.9570 - learning_rate: 5.0000e-04
## Epoch 111/500
## 90/90 - 0s - 2ms/step - loss: 0.0786 - sparse_categorical_accuracy: 0.9740 - val_loss: 0.1254 - val_sparse_categorical_accuracy: 0.9445 - learning_rate: 5.0000e-04
## Epoch 112/500
## 90/90 - 0s - 2ms/step - loss: 0.0801 - sparse_categorical_accuracy: 0.9753 - val_loss: 0.1339 - val_sparse_categorical_accuracy: 0.9445 - learning_rate: 5.0000e-04
## Epoch 113/500
## 90/90 - 0s - 2ms/step - loss: 0.0751 - sparse_categorical_accuracy: 0.9764 - val_loss: 0.1334 - val_sparse_categorical_accuracy: 0.9431 - learning_rate: 5.0000e-04
## Epoch 114/500
## 90/90 - 0s - 1ms/step - loss: 0.0909 - sparse_categorical_accuracy: 0.9691 - val_loss: 0.1166 - val_sparse_categorical_accuracy: 0.9612 - learning_rate: 5.0000e-04
## Epoch 115/500
## 90/90 - 0s - 2ms/step - loss: 0.0730 - sparse_categorical_accuracy: 0.9760 - val_loss: 0.1177 - val_sparse_categorical_accuracy: 0.9459 - learning_rate: 5.0000e-04
## Epoch 116/500
## 90/90 - 0s - 2ms/step - loss: 0.0798 - sparse_categorical_accuracy: 0.9743 - val_loss: 0.1339 - val_sparse_categorical_accuracy: 0.9487 - learning_rate: 5.0000e-04
## Epoch 117/500
## 90/90 - 0s - 1ms/step - loss: 0.0808 - sparse_categorical_accuracy: 0.9729 - val_loss: 0.1381 - val_sparse_categorical_accuracy: 0.9556 - learning_rate: 5.0000e-04
## Epoch 118/500
## 90/90 - 0s - 2ms/step - loss: 0.0786 - sparse_categorical_accuracy: 0.9750 - val_loss: 0.2099 - val_sparse_categorical_accuracy: 0.9237 - learning_rate: 5.0000e-04
## Epoch 119/500
## 90/90 - 0s - 1ms/step - loss: 0.0783 - sparse_categorical_accuracy: 0.9740 - val_loss: 0.1106 - val_sparse_categorical_accuracy: 0.9584 - learning_rate: 5.0000e-04
## Epoch 120/500
## 90/90 - 0s - 2ms/step - loss: 0.0810 - sparse_categorical_accuracy: 0.9750 - val_loss: 0.5614 - val_sparse_categorical_accuracy: 0.8239 - learning_rate: 5.0000e-04
## Epoch 121/500
## 90/90 - 0s - 1ms/step - loss: 0.0757 - sparse_categorical_accuracy: 0.9767 - val_loss: 0.1111 - val_sparse_categorical_accuracy: 0.9584 - learning_rate: 5.0000e-04
## Epoch 122/500
## 90/90 - 0s - 2ms/step - loss: 0.0781 - sparse_categorical_accuracy: 0.9733 - val_loss: 0.1082 - val_sparse_categorical_accuracy: 0.9639 - learning_rate: 5.0000e-04
## Epoch 123/500
## 90/90 - 0s - 1ms/step - loss: 0.0777 - sparse_categorical_accuracy: 0.9753 - val_loss: 0.1205 - val_sparse_categorical_accuracy: 0.9570 - learning_rate: 5.0000e-04
## Epoch 124/500
## 90/90 - 0s - 2ms/step - loss: 0.0855 - sparse_categorical_accuracy: 0.9701 - val_loss: 0.1416 - val_sparse_categorical_accuracy: 0.9390 - learning_rate: 5.0000e-04
## Epoch 125/500
## 90/90 - 0s - 1ms/step - loss: 0.0824 - sparse_categorical_accuracy: 0.9712 - val_loss: 0.1124 - val_sparse_categorical_accuracy: 0.9653 - learning_rate: 5.0000e-04
## Epoch 126/500
## 90/90 - 0s - 1ms/step - loss: 0.0773 - sparse_categorical_accuracy: 0.9733 - val_loss: 0.1519 - val_sparse_categorical_accuracy: 0.9515 - learning_rate: 5.0000e-04
## Epoch 127/500
## 90/90 - 0s - 2ms/step - loss: 0.0753 - sparse_categorical_accuracy: 0.9799 - val_loss: 0.2766 - val_sparse_categorical_accuracy: 0.9043 - learning_rate: 5.0000e-04
## Epoch 128/500
## 90/90 - 0s - 2ms/step - loss: 0.0773 - sparse_categorical_accuracy: 0.9743 - val_loss: 0.1165 - val_sparse_categorical_accuracy: 0.9515 - learning_rate: 5.0000e-04
## Epoch 129/500
## 90/90 - 0s - 2ms/step - loss: 0.0795 - sparse_categorical_accuracy: 0.9726 - val_loss: 0.1374 - val_sparse_categorical_accuracy: 0.9556 - learning_rate: 5.0000e-04
## Epoch 130/500
## 90/90 - 0s - 2ms/step - loss: 0.0857 - sparse_categorical_accuracy: 0.9722 - val_loss: 0.1607 - val_sparse_categorical_accuracy: 0.9320 - learning_rate: 5.0000e-04
## Epoch 131/500
## 90/90 - 0s - 1ms/step - loss: 0.0746 - sparse_categorical_accuracy: 0.9781 - val_loss: 0.1141 - val_sparse_categorical_accuracy: 0.9598 - learning_rate: 5.0000e-04
## Epoch 132/500
## 90/90 - 0s - 2ms/step - loss: 0.0736 - sparse_categorical_accuracy: 0.9747 - val_loss: 0.1164 - val_sparse_categorical_accuracy: 0.9626 - learning_rate: 5.0000e-04
## Epoch 133/500
## 90/90 - 0s - 2ms/step - loss: 0.0678 - sparse_categorical_accuracy: 0.9757 - val_loss: 0.1690 - val_sparse_categorical_accuracy: 0.9417 - learning_rate: 5.0000e-04
## Epoch 134/500
## 90/90 - 0s - 2ms/step - loss: 0.0760 - sparse_categorical_accuracy: 0.9753 - val_loss: 0.1666 - val_sparse_categorical_accuracy: 0.9417 - learning_rate: 5.0000e-04
## Epoch 135/500
## 90/90 - 0s - 2ms/step - loss: 0.0753 - sparse_categorical_accuracy: 0.9757 - val_loss: 0.1821 - val_sparse_categorical_accuracy: 0.9334 - learning_rate: 5.0000e-04
## Epoch 136/500
## 90/90 - 0s - 2ms/step - loss: 0.0785 - sparse_categorical_accuracy: 0.9719 - val_loss: 0.1089 - val_sparse_categorical_accuracy: 0.9667 - learning_rate: 5.0000e-04
## Epoch 137/500
## 90/90 - 0s - 2ms/step - loss: 0.0834 - sparse_categorical_accuracy: 0.9708 - val_loss: 0.2068 - val_sparse_categorical_accuracy: 0.9182 - learning_rate: 5.0000e-04
## Epoch 138/500
## 90/90 - 0s - 2ms/step - loss: 0.0755 - sparse_categorical_accuracy: 0.9747 - val_loss: 0.1211 - val_sparse_categorical_accuracy: 0.9445 - learning_rate: 5.0000e-04
## Epoch 139/500
## 90/90 - 0s - 2ms/step - loss: 0.0844 - sparse_categorical_accuracy: 0.9722 - val_loss: 0.1159 - val_sparse_categorical_accuracy: 0.9584 - learning_rate: 5.0000e-04
## Epoch 140/500
## 90/90 - 0s - 2ms/step - loss: 0.0719 - sparse_categorical_accuracy: 0.9778 - val_loss: 0.1473 - val_sparse_categorical_accuracy: 0.9404 - learning_rate: 5.0000e-04
## Epoch 141/500
## 90/90 - 0s - 2ms/step - loss: 0.0743 - sparse_categorical_accuracy: 0.9750 - val_loss: 0.1458 - val_sparse_categorical_accuracy: 0.9362 - learning_rate: 5.0000e-04
## Epoch 142/500
## 90/90 - 0s - 2ms/step - loss: 0.0692 - sparse_categorical_accuracy: 0.9809 - val_loss: 0.1058 - val_sparse_categorical_accuracy: 0.9626 - learning_rate: 5.0000e-04
## Epoch 143/500
## 90/90 - 0s - 2ms/step - loss: 0.0744 - sparse_categorical_accuracy: 0.9750 - val_loss: 0.1628 - val_sparse_categorical_accuracy: 0.9417 - learning_rate: 5.0000e-04
## Epoch 144/500
## 90/90 - 0s - 2ms/step - loss: 0.0679 - sparse_categorical_accuracy: 0.9799 - val_loss: 0.1912 - val_sparse_categorical_accuracy: 0.9140 - learning_rate: 5.0000e-04
## Epoch 145/500
## 90/90 - 0s - 2ms/step - loss: 0.0721 - sparse_categorical_accuracy: 0.9750 - val_loss: 0.1965 - val_sparse_categorical_accuracy: 0.9223 - learning_rate: 5.0000e-04
## Epoch 146/500
## 90/90 - 0s - 2ms/step - loss: 0.0746 - sparse_categorical_accuracy: 0.9740 - val_loss: 0.1597 - val_sparse_categorical_accuracy: 0.9376 - learning_rate: 5.0000e-04
## Epoch 147/500
## 90/90 - 0s - 2ms/step - loss: 0.0795 - sparse_categorical_accuracy: 0.9747 - val_loss: 0.1149 - val_sparse_categorical_accuracy: 0.9501 - learning_rate: 5.0000e-04
## Epoch 148/500
## 90/90 - 0s - 2ms/step - loss: 0.0831 - sparse_categorical_accuracy: 0.9736 - val_loss: 0.2469 - val_sparse_categorical_accuracy: 0.9043 - learning_rate: 5.0000e-04
## Epoch 149/500
## 90/90 - 0s - 2ms/step - loss: 0.0735 - sparse_categorical_accuracy: 0.9757 - val_loss: 0.1411 - val_sparse_categorical_accuracy: 0.9473 - learning_rate: 5.0000e-04
## Epoch 150/500
## 90/90 - 0s - 1ms/step - loss: 0.0746 - sparse_categorical_accuracy: 0.9750 - val_loss: 0.2120 - val_sparse_categorical_accuracy: 0.9237 - learning_rate: 5.0000e-04
## Epoch 151/500
## 90/90 - 0s - 2ms/step - loss: 0.0708 - sparse_categorical_accuracy: 0.9771 - val_loss: 0.2874 - val_sparse_categorical_accuracy: 0.8918 - learning_rate: 5.0000e-04
## Epoch 152/500
## 90/90 - 0s - 2ms/step - loss: 0.0735 - sparse_categorical_accuracy: 0.9736 - val_loss: 0.1421 - val_sparse_categorical_accuracy: 0.9404 - learning_rate: 5.0000e-04
## Epoch 153/500
## 90/90 - 0s - 2ms/step - loss: 0.0712 - sparse_categorical_accuracy: 0.9767 - val_loss: 0.1572 - val_sparse_categorical_accuracy: 0.9334 - learning_rate: 5.0000e-04
## Epoch 154/500
## 90/90 - 0s - 2ms/step - loss: 0.0687 - sparse_categorical_accuracy: 0.9774 - val_loss: 0.1060 - val_sparse_categorical_accuracy: 0.9626 - learning_rate: 5.0000e-04
## Epoch 155/500
## 90/90 - 0s - 2ms/step - loss: 0.0705 - sparse_categorical_accuracy: 0.9774 - val_loss: 0.1114 - val_sparse_categorical_accuracy: 0.9556 - learning_rate: 5.0000e-04
## Epoch 156/500
## 90/90 - 0s - 2ms/step - loss: 0.0736 - sparse_categorical_accuracy: 0.9764 - val_loss: 0.1364 - val_sparse_categorical_accuracy: 0.9445 - learning_rate: 5.0000e-04
## Epoch 157/500
## 90/90 - 0s - 2ms/step - loss: 0.0709 - sparse_categorical_accuracy: 0.9722 - val_loss: 0.1086 - val_sparse_categorical_accuracy: 0.9639 - learning_rate: 5.0000e-04
## Epoch 158/500
## 90/90 - 0s - 2ms/step - loss: 0.0713 - sparse_categorical_accuracy: 0.9760 - val_loss: 0.1254 - val_sparse_categorical_accuracy: 0.9598 - learning_rate: 5.0000e-04
## Epoch 159/500
## 90/90 - 0s - 2ms/step - loss: 0.0708 - sparse_categorical_accuracy: 0.9767 - val_loss: 0.2376 - val_sparse_categorical_accuracy: 0.9043 - learning_rate: 5.0000e-04
## Epoch 160/500
## 90/90 - 0s - 2ms/step - loss: 0.0741 - sparse_categorical_accuracy: 0.9747 - val_loss: 0.2060 - val_sparse_categorical_accuracy: 0.9196 - learning_rate: 5.0000e-04
## Epoch 161/500
## 90/90 - 0s - 2ms/step - loss: 0.0687 - sparse_categorical_accuracy: 0.9750 - val_loss: 0.1326 - val_sparse_categorical_accuracy: 0.9445 - learning_rate: 5.0000e-04
## Epoch 162/500
## 90/90 - 0s - 1ms/step - loss: 0.0667 - sparse_categorical_accuracy: 0.9771 - val_loss: 0.1525 - val_sparse_categorical_accuracy: 0.9487 - learning_rate: 5.0000e-04
## Epoch 163/500
## 90/90 - 0s - 1ms/step - loss: 0.0601 - sparse_categorical_accuracy: 0.9802 - val_loss: 0.1215 - val_sparse_categorical_accuracy: 0.9612 - learning_rate: 2.5000e-04
## Epoch 164/500
## 90/90 - 0s - 2ms/step - loss: 0.0632 - sparse_categorical_accuracy: 0.9809 - val_loss: 0.1007 - val_sparse_categorical_accuracy: 0.9653 - learning_rate: 2.5000e-04
## Epoch 165/500
## 90/90 - 0s - 1ms/step - loss: 0.0610 - sparse_categorical_accuracy: 0.9823 - val_loss: 0.1018 - val_sparse_categorical_accuracy: 0.9681 - learning_rate: 2.5000e-04
## Epoch 166/500
## 90/90 - 0s - 2ms/step - loss: 0.0584 - sparse_categorical_accuracy: 0.9816 - val_loss: 0.1005 - val_sparse_categorical_accuracy: 0.9626 - learning_rate: 2.5000e-04
## Epoch 167/500
## 90/90 - 0s - 2ms/step - loss: 0.0603 - sparse_categorical_accuracy: 0.9806 - val_loss: 0.1010 - val_sparse_categorical_accuracy: 0.9653 - learning_rate: 2.5000e-04
## Epoch 168/500
## 90/90 - 0s - 1ms/step - loss: 0.0704 - sparse_categorical_accuracy: 0.9760 - val_loss: 0.1150 - val_sparse_categorical_accuracy: 0.9598 - learning_rate: 2.5000e-04
## Epoch 169/500
## 90/90 - 0s - 1ms/step - loss: 0.0624 - sparse_categorical_accuracy: 0.9792 - val_loss: 0.1057 - val_sparse_categorical_accuracy: 0.9570 - learning_rate: 2.5000e-04
## Epoch 170/500
## 90/90 - 0s - 1ms/step - loss: 0.0629 - sparse_categorical_accuracy: 0.9813 - val_loss: 0.1027 - val_sparse_categorical_accuracy: 0.9584 - learning_rate: 2.5000e-04
## Epoch 171/500
## 90/90 - 0s - 1ms/step - loss: 0.0588 - sparse_categorical_accuracy: 0.9795 - val_loss: 0.1238 - val_sparse_categorical_accuracy: 0.9556 - learning_rate: 2.5000e-04
## Epoch 172/500
## 90/90 - 0s - 1ms/step - loss: 0.0604 - sparse_categorical_accuracy: 0.9792 - val_loss: 0.1050 - val_sparse_categorical_accuracy: 0.9667 - learning_rate: 2.5000e-04
## Epoch 173/500
## 90/90 - 0s - 1ms/step - loss: 0.0598 - sparse_categorical_accuracy: 0.9819 - val_loss: 0.1461 - val_sparse_categorical_accuracy: 0.9459 - learning_rate: 2.5000e-04
## Epoch 174/500
## 90/90 - 0s - 2ms/step - loss: 0.0625 - sparse_categorical_accuracy: 0.9771 - val_loss: 0.1207 - val_sparse_categorical_accuracy: 0.9487 - learning_rate: 2.5000e-04
## Epoch 175/500
## 90/90 - 0s - 2ms/step - loss: 0.0630 - sparse_categorical_accuracy: 0.9788 - val_loss: 0.1034 - val_sparse_categorical_accuracy: 0.9653 - learning_rate: 2.5000e-04
## Epoch 176/500
## 90/90 - 0s - 1ms/step - loss: 0.0624 - sparse_categorical_accuracy: 0.9774 - val_loss: 0.1080 - val_sparse_categorical_accuracy: 0.9653 - learning_rate: 2.5000e-04
## Epoch 177/500
## 90/90 - 0s - 1ms/step - loss: 0.0593 - sparse_categorical_accuracy: 0.9813 - val_loss: 0.1233 - val_sparse_categorical_accuracy: 0.9584 - learning_rate: 2.5000e-04
## Epoch 178/500
## 90/90 - 0s - 1ms/step - loss: 0.0575 - sparse_categorical_accuracy: 0.9816 - val_loss: 0.1626 - val_sparse_categorical_accuracy: 0.9348 - learning_rate: 2.5000e-04
## Epoch 179/500
## 90/90 - 0s - 2ms/step - loss: 0.0580 - sparse_categorical_accuracy: 0.9802 - val_loss: 0.1437 - val_sparse_categorical_accuracy: 0.9515 - learning_rate: 2.5000e-04
## Epoch 180/500
## 90/90 - 0s - 1ms/step - loss: 0.0581 - sparse_categorical_accuracy: 0.9830 - val_loss: 0.1635 - val_sparse_categorical_accuracy: 0.9445 - learning_rate: 2.5000e-04
## Epoch 181/500
## 90/90 - 0s - 2ms/step - loss: 0.0625 - sparse_categorical_accuracy: 0.9823 - val_loss: 0.1218 - val_sparse_categorical_accuracy: 0.9626 - learning_rate: 2.5000e-04
## Epoch 182/500
## 90/90 - 0s - 2ms/step - loss: 0.0575 - sparse_categorical_accuracy: 0.9830 - val_loss: 0.1320 - val_sparse_categorical_accuracy: 0.9542 - learning_rate: 2.5000e-04
## Epoch 183/500
## 90/90 - 0s - 1ms/step - loss: 0.0607 - sparse_categorical_accuracy: 0.9788 - val_loss: 0.1015 - val_sparse_categorical_accuracy: 0.9626 - learning_rate: 2.5000e-04
## Epoch 184/500
## 90/90 - 0s - 1ms/step - loss: 0.0558 - sparse_categorical_accuracy: 0.9819 - val_loss: 0.1052 - val_sparse_categorical_accuracy: 0.9556 - learning_rate: 2.5000e-04
## Epoch 185/500
## 90/90 - 0s - 1ms/step - loss: 0.0587 - sparse_categorical_accuracy: 0.9816 - val_loss: 0.1075 - val_sparse_categorical_accuracy: 0.9612 - learning_rate: 2.5000e-04
## Epoch 186/500
## 90/90 - 0s - 1ms/step - loss: 0.0651 - sparse_categorical_accuracy: 0.9792 - val_loss: 0.1085 - val_sparse_categorical_accuracy: 0.9639 - learning_rate: 2.5000e-04
## Epoch 187/500
## 90/90 - 0s - 2ms/step - loss: 0.0560 - sparse_categorical_accuracy: 0.9809 - val_loss: 0.0999 - val_sparse_categorical_accuracy: 0.9681 - learning_rate: 1.2500e-04
## Epoch 188/500
## 90/90 - 0s - 2ms/step - loss: 0.0549 - sparse_categorical_accuracy: 0.9844 - val_loss: 0.1025 - val_sparse_categorical_accuracy: 0.9709 - learning_rate: 1.2500e-04
## Epoch 189/500
## 90/90 - 0s - 1ms/step - loss: 0.0522 - sparse_categorical_accuracy: 0.9844 - val_loss: 0.1051 - val_sparse_categorical_accuracy: 0.9695 - learning_rate: 1.2500e-04
## Epoch 190/500
## 90/90 - 0s - 2ms/step - loss: 0.0603 - sparse_categorical_accuracy: 0.9806 - val_loss: 0.1249 - val_sparse_categorical_accuracy: 0.9570 - learning_rate: 1.2500e-04
## Epoch 191/500
## 90/90 - 0s - 2ms/step - loss: 0.0545 - sparse_categorical_accuracy: 0.9823 - val_loss: 0.0988 - val_sparse_categorical_accuracy: 0.9653 - learning_rate: 1.2500e-04
## Epoch 192/500
## 90/90 - 0s - 2ms/step - loss: 0.0591 - sparse_categorical_accuracy: 0.9799 - val_loss: 0.1063 - val_sparse_categorical_accuracy: 0.9639 - learning_rate: 1.2500e-04
## Epoch 193/500
## 90/90 - 0s - 2ms/step - loss: 0.0561 - sparse_categorical_accuracy: 0.9830 - val_loss: 0.1141 - val_sparse_categorical_accuracy: 0.9598 - learning_rate: 1.2500e-04
## Epoch 194/500
## 90/90 - 0s - 1ms/step - loss: 0.0548 - sparse_categorical_accuracy: 0.9819 - val_loss: 0.1112 - val_sparse_categorical_accuracy: 0.9626 - learning_rate: 1.2500e-04
## Epoch 195/500
## 90/90 - 0s - 1ms/step - loss: 0.0544 - sparse_categorical_accuracy: 0.9833 - val_loss: 0.1079 - val_sparse_categorical_accuracy: 0.9626 - learning_rate: 1.2500e-04
## Epoch 196/500
## 90/90 - 0s - 1ms/step - loss: 0.0573 - sparse_categorical_accuracy: 0.9809 - val_loss: 0.1004 - val_sparse_categorical_accuracy: 0.9681 - learning_rate: 1.2500e-04
## Epoch 197/500
## 90/90 - 0s - 2ms/step - loss: 0.0537 - sparse_categorical_accuracy: 0.9833 - val_loss: 0.0976 - val_sparse_categorical_accuracy: 0.9639 - learning_rate: 1.2500e-04
## Epoch 198/500
## 90/90 - 0s - 2ms/step - loss: 0.0537 - sparse_categorical_accuracy: 0.9854 - val_loss: 0.0985 - val_sparse_categorical_accuracy: 0.9653 - learning_rate: 1.2500e-04
## Epoch 199/500
## 90/90 - 0s - 2ms/step - loss: 0.0565 - sparse_categorical_accuracy: 0.9819 - val_loss: 0.0983 - val_sparse_categorical_accuracy: 0.9695 - learning_rate: 1.2500e-04
## Epoch 200/500
## 90/90 - 0s - 1ms/step - loss: 0.0563 - sparse_categorical_accuracy: 0.9830 - val_loss: 0.1007 - val_sparse_categorical_accuracy: 0.9667 - learning_rate: 1.2500e-04
## Epoch 201/500
## 90/90 - 0s - 2ms/step - loss: 0.0543 - sparse_categorical_accuracy: 0.9799 - val_loss: 0.1094 - val_sparse_categorical_accuracy: 0.9709 - learning_rate: 1.2500e-04
## Epoch 202/500
## 90/90 - 0s - 2ms/step - loss: 0.0543 - sparse_categorical_accuracy: 0.9833 - val_loss: 0.1147 - val_sparse_categorical_accuracy: 0.9626 - learning_rate: 1.2500e-04
## Epoch 203/500
## 90/90 - 0s - 2ms/step - loss: 0.0554 - sparse_categorical_accuracy: 0.9837 - val_loss: 0.1105 - val_sparse_categorical_accuracy: 0.9626 - learning_rate: 1.2500e-04
## Epoch 204/500
## 90/90 - 0s - 2ms/step - loss: 0.0507 - sparse_categorical_accuracy: 0.9844 - val_loss: 0.0998 - val_sparse_categorical_accuracy: 0.9639 - learning_rate: 1.2500e-04
## Epoch 205/500
## 90/90 - 0s - 2ms/step - loss: 0.0540 - sparse_categorical_accuracy: 0.9823 - val_loss: 0.1004 - val_sparse_categorical_accuracy: 0.9626 - learning_rate: 1.2500e-04
## Epoch 206/500
## 90/90 - 0s - 1ms/step - loss: 0.0543 - sparse_categorical_accuracy: 0.9826 - val_loss: 0.0994 - val_sparse_categorical_accuracy: 0.9667 - learning_rate: 1.2500e-04
## Epoch 207/500
## 90/90 - 0s - 1ms/step - loss: 0.0581 - sparse_categorical_accuracy: 0.9813 - val_loss: 0.1018 - val_sparse_categorical_accuracy: 0.9598 - learning_rate: 1.2500e-04
## Epoch 208/500
## 90/90 - 0s - 2ms/step - loss: 0.0540 - sparse_categorical_accuracy: 0.9830 - val_loss: 0.1238 - val_sparse_categorical_accuracy: 0.9584 - learning_rate: 1.2500e-04
## Epoch 209/500
## 90/90 - 0s - 2ms/step - loss: 0.0526 - sparse_categorical_accuracy: 0.9816 - val_loss: 0.1196 - val_sparse_categorical_accuracy: 0.9612 - learning_rate: 1.2500e-04
## Epoch 210/500
## 90/90 - 0s - 2ms/step - loss: 0.0563 - sparse_categorical_accuracy: 0.9813 - val_loss: 0.0997 - val_sparse_categorical_accuracy: 0.9570 - learning_rate: 1.2500e-04
## Epoch 211/500
## 90/90 - 0s - 2ms/step - loss: 0.0541 - sparse_categorical_accuracy: 0.9826 - val_loss: 0.0976 - val_sparse_categorical_accuracy: 0.9681 - learning_rate: 1.2500e-04
## Epoch 212/500
## 90/90 - 0s - 1ms/step - loss: 0.0530 - sparse_categorical_accuracy: 0.9854 - val_loss: 0.1003 - val_sparse_categorical_accuracy: 0.9709 - learning_rate: 1.2500e-04
## Epoch 213/500
## 90/90 - 0s - 2ms/step - loss: 0.0561 - sparse_categorical_accuracy: 0.9823 - val_loss: 0.0962 - val_sparse_categorical_accuracy: 0.9639 - learning_rate: 1.2500e-04
## Epoch 214/500
## 90/90 - 0s - 2ms/step - loss: 0.0551 - sparse_categorical_accuracy: 0.9823 - val_loss: 0.1040 - val_sparse_categorical_accuracy: 0.9653 - learning_rate: 1.2500e-04
## Epoch 215/500
## 90/90 - 0s - 2ms/step - loss: 0.0526 - sparse_categorical_accuracy: 0.9813 - val_loss: 0.1068 - val_sparse_categorical_accuracy: 0.9667 - learning_rate: 1.2500e-04
## Epoch 216/500
## 90/90 - 0s - 2ms/step - loss: 0.0517 - sparse_categorical_accuracy: 0.9840 - val_loss: 0.1011 - val_sparse_categorical_accuracy: 0.9653 - learning_rate: 1.2500e-04
## Epoch 217/500
## 90/90 - 0s - 2ms/step - loss: 0.0522 - sparse_categorical_accuracy: 0.9819 - val_loss: 0.1200 - val_sparse_categorical_accuracy: 0.9612 - learning_rate: 1.2500e-04
## Epoch 218/500
## 90/90 - 0s - 2ms/step - loss: 0.0563 - sparse_categorical_accuracy: 0.9819 - val_loss: 0.0980 - val_sparse_categorical_accuracy: 0.9667 - learning_rate: 1.2500e-04
## Epoch 219/500
## 90/90 - 0s - 1ms/step - loss: 0.0539 - sparse_categorical_accuracy: 0.9844 - val_loss: 0.1071 - val_sparse_categorical_accuracy: 0.9626 - learning_rate: 1.2500e-04
## Epoch 220/500
## 90/90 - 0s - 2ms/step - loss: 0.0529 - sparse_categorical_accuracy: 0.9833 - val_loss: 0.1006 - val_sparse_categorical_accuracy: 0.9695 - learning_rate: 1.2500e-04
## Epoch 221/500
## 90/90 - 0s - 2ms/step - loss: 0.0552 - sparse_categorical_accuracy: 0.9799 - val_loss: 0.1067 - val_sparse_categorical_accuracy: 0.9626 - learning_rate: 1.2500e-04
## Epoch 222/500
## 90/90 - 0s - 2ms/step - loss: 0.0545 - sparse_categorical_accuracy: 0.9806 - val_loss: 0.0962 - val_sparse_categorical_accuracy: 0.9667 - learning_rate: 1.2500e-04
## Epoch 223/500
## 90/90 - 0s - 2ms/step - loss: 0.0541 - sparse_categorical_accuracy: 0.9833 - val_loss: 0.0970 - val_sparse_categorical_accuracy: 0.9667 - learning_rate: 1.2500e-04
## Epoch 224/500
## 90/90 - 0s - 2ms/step - loss: 0.0507 - sparse_categorical_accuracy: 0.9854 - val_loss: 0.1081 - val_sparse_categorical_accuracy: 0.9584 - learning_rate: 1.2500e-04
## Epoch 225/500
## 90/90 - 0s - 2ms/step - loss: 0.0551 - sparse_categorical_accuracy: 0.9847 - val_loss: 0.1393 - val_sparse_categorical_accuracy: 0.9528 - learning_rate: 1.2500e-04
## Epoch 226/500
## 90/90 - 0s - 2ms/step - loss: 0.0500 - sparse_categorical_accuracy: 0.9837 - val_loss: 0.1245 - val_sparse_categorical_accuracy: 0.9542 - learning_rate: 1.2500e-04
## Epoch 227/500
## 90/90 - 0s - 2ms/step - loss: 0.0549 - sparse_categorical_accuracy: 0.9809 - val_loss: 0.1016 - val_sparse_categorical_accuracy: 0.9639 - learning_rate: 1.2500e-04
## Epoch 228/500
## 90/90 - 0s - 2ms/step - loss: 0.0501 - sparse_categorical_accuracy: 0.9851 - val_loss: 0.1016 - val_sparse_categorical_accuracy: 0.9626 - learning_rate: 1.2500e-04
## Epoch 229/500
## 90/90 - 0s - 2ms/step - loss: 0.0506 - sparse_categorical_accuracy: 0.9861 - val_loss: 0.0955 - val_sparse_categorical_accuracy: 0.9681 - learning_rate: 1.2500e-04
## Epoch 230/500
## 90/90 - 0s - 2ms/step - loss: 0.0511 - sparse_categorical_accuracy: 0.9858 - val_loss: 0.1009 - val_sparse_categorical_accuracy: 0.9598 - learning_rate: 1.2500e-04
## Epoch 231/500
## 90/90 - 0s - 2ms/step - loss: 0.0548 - sparse_categorical_accuracy: 0.9809 - val_loss: 0.0990 - val_sparse_categorical_accuracy: 0.9598 - learning_rate: 1.2500e-04
## Epoch 232/500
## 90/90 - 0s - 2ms/step - loss: 0.0513 - sparse_categorical_accuracy: 0.9858 - val_loss: 0.0967 - val_sparse_categorical_accuracy: 0.9667 - learning_rate: 1.2500e-04
## Epoch 233/500
## 90/90 - 0s - 2ms/step - loss: 0.0523 - sparse_categorical_accuracy: 0.9847 - val_loss: 0.1001 - val_sparse_categorical_accuracy: 0.9626 - learning_rate: 1.2500e-04
## Epoch 234/500
## 90/90 - 0s - 2ms/step - loss: 0.0521 - sparse_categorical_accuracy: 0.9844 - val_loss: 0.1489 - val_sparse_categorical_accuracy: 0.9487 - learning_rate: 1.2500e-04
## Epoch 235/500
## 90/90 - 0s - 2ms/step - loss: 0.0520 - sparse_categorical_accuracy: 0.9813 - val_loss: 0.1173 - val_sparse_categorical_accuracy: 0.9570 - learning_rate: 1.2500e-04
## Epoch 236/500
## 90/90 - 0s - 1ms/step - loss: 0.0540 - sparse_categorical_accuracy: 0.9806 - val_loss: 0.0995 - val_sparse_categorical_accuracy: 0.9681 - learning_rate: 1.2500e-04
## Epoch 237/500
## 90/90 - 0s - 2ms/step - loss: 0.0534 - sparse_categorical_accuracy: 0.9813 - val_loss: 0.1324 - val_sparse_categorical_accuracy: 0.9556 - learning_rate: 1.2500e-04
## Epoch 238/500
## 90/90 - 0s - 2ms/step - loss: 0.0516 - sparse_categorical_accuracy: 0.9861 - val_loss: 0.1064 - val_sparse_categorical_accuracy: 0.9681 - learning_rate: 1.2500e-04
## Epoch 239/500
## 90/90 - 0s - 2ms/step - loss: 0.0517 - sparse_categorical_accuracy: 0.9847 - val_loss: 0.1002 - val_sparse_categorical_accuracy: 0.9639 - learning_rate: 1.2500e-04
## Epoch 240/500
## 90/90 - 0s - 2ms/step - loss: 0.0506 - sparse_categorical_accuracy: 0.9844 - val_loss: 0.1461 - val_sparse_categorical_accuracy: 0.9431 - learning_rate: 1.2500e-04
## Epoch 241/500
## 90/90 - 0s - 2ms/step - loss: 0.0528 - sparse_categorical_accuracy: 0.9837 - val_loss: 0.1036 - val_sparse_categorical_accuracy: 0.9626 - learning_rate: 1.2500e-04
## Epoch 242/500
## 90/90 - 0s - 1ms/step - loss: 0.0525 - sparse_categorical_accuracy: 0.9837 - val_loss: 0.1165 - val_sparse_categorical_accuracy: 0.9584 - learning_rate: 1.2500e-04
## Epoch 243/500
## 90/90 - 0s - 1ms/step - loss: 0.0547 - sparse_categorical_accuracy: 0.9802 - val_loss: 0.0972 - val_sparse_categorical_accuracy: 0.9639 - learning_rate: 1.2500e-04
## Epoch 244/500
## 90/90 - 0s - 2ms/step - loss: 0.0554 - sparse_categorical_accuracy: 0.9806 - val_loss: 0.1206 - val_sparse_categorical_accuracy: 0.9584 - learning_rate: 1.2500e-04
## Epoch 245/500
## 90/90 - 0s - 2ms/step - loss: 0.0518 - sparse_categorical_accuracy: 0.9830 - val_loss: 0.1057 - val_sparse_categorical_accuracy: 0.9639 - learning_rate: 1.2500e-04
## Epoch 246/500
## 90/90 - 0s - 2ms/step - loss: 0.0527 - sparse_categorical_accuracy: 0.9833 - val_loss: 0.0974 - val_sparse_categorical_accuracy: 0.9653 - learning_rate: 1.2500e-04
## Epoch 247/500
## 90/90 - 0s - 2ms/step - loss: 0.0481 - sparse_categorical_accuracy: 0.9844 - val_loss: 0.0970 - val_sparse_categorical_accuracy: 0.9681 - learning_rate: 1.2500e-04
## Epoch 248/500
## 90/90 - 0s - 2ms/step - loss: 0.0479 - sparse_categorical_accuracy: 0.9865 - val_loss: 0.0983 - val_sparse_categorical_accuracy: 0.9667 - learning_rate: 1.2500e-04
## Epoch 249/500
## 90/90 - 0s - 2ms/step - loss: 0.0525 - sparse_categorical_accuracy: 0.9861 - val_loss: 0.1533 - val_sparse_categorical_accuracy: 0.9376 - learning_rate: 1.2500e-04
## Epoch 250/500
## 90/90 - 0s - 2ms/step - loss: 0.0532 - sparse_categorical_accuracy: 0.9809 - val_loss: 0.0995 - val_sparse_categorical_accuracy: 0.9681 - learning_rate: 1.0000e-04
## Epoch 251/500
## 90/90 - 0s - 1ms/step - loss: 0.0508 - sparse_categorical_accuracy: 0.9830 - val_loss: 0.1049 - val_sparse_categorical_accuracy: 0.9667 - learning_rate: 1.0000e-04
## Epoch 252/500
## 90/90 - 0s - 1ms/step - loss: 0.0522 - sparse_categorical_accuracy: 0.9837 - val_loss: 0.1094 - val_sparse_categorical_accuracy: 0.9653 - learning_rate: 1.0000e-04
## Epoch 253/500
## 90/90 - 0s - 1ms/step - loss: 0.0515 - sparse_categorical_accuracy: 0.9847 - val_loss: 0.1032 - val_sparse_categorical_accuracy: 0.9626 - learning_rate: 1.0000e-04
## Epoch 254/500
## 90/90 - 0s - 1ms/step - loss: 0.0529 - sparse_categorical_accuracy: 0.9830 - val_loss: 0.1047 - val_sparse_categorical_accuracy: 0.9598 - learning_rate: 1.0000e-04
## Epoch 255/500
## 90/90 - 0s - 2ms/step - loss: 0.0494 - sparse_categorical_accuracy: 0.9819 - val_loss: 0.0951 - val_sparse_categorical_accuracy: 0.9667 - learning_rate: 1.0000e-04
## Epoch 256/500
## 90/90 - 0s - 2ms/step - loss: 0.0508 - sparse_categorical_accuracy: 0.9861 - val_loss: 0.0986 - val_sparse_categorical_accuracy: 0.9653 - learning_rate: 1.0000e-04
## Epoch 257/500
## 90/90 - 0s - 1ms/step - loss: 0.0500 - sparse_categorical_accuracy: 0.9851 - val_loss: 0.0990 - val_sparse_categorical_accuracy: 0.9653 - learning_rate: 1.0000e-04
## Epoch 258/500
## 90/90 - 0s - 2ms/step - loss: 0.0473 - sparse_categorical_accuracy: 0.9872 - val_loss: 0.1037 - val_sparse_categorical_accuracy: 0.9653 - learning_rate: 1.0000e-04
## Epoch 259/500
## 90/90 - 0s - 1ms/step - loss: 0.0477 - sparse_categorical_accuracy: 0.9865 - val_loss: 0.1000 - val_sparse_categorical_accuracy: 0.9667 - learning_rate: 1.0000e-04
## Epoch 260/500
## 90/90 - 0s - 2ms/step - loss: 0.0478 - sparse_categorical_accuracy: 0.9865 - val_loss: 0.0962 - val_sparse_categorical_accuracy: 0.9626 - learning_rate: 1.0000e-04
## Epoch 261/500
## 90/90 - 0s - 2ms/step - loss: 0.0509 - sparse_categorical_accuracy: 0.9816 - val_loss: 0.1077 - val_sparse_categorical_accuracy: 0.9681 - learning_rate: 1.0000e-04
## Epoch 262/500
## 90/90 - 0s - 2ms/step - loss: 0.0485 - sparse_categorical_accuracy: 0.9851 - val_loss: 0.0975 - val_sparse_categorical_accuracy: 0.9653 - learning_rate: 1.0000e-04
## Epoch 263/500
## 90/90 - 0s - 2ms/step - loss: 0.0479 - sparse_categorical_accuracy: 0.9847 - val_loss: 0.0973 - val_sparse_categorical_accuracy: 0.9639 - learning_rate: 1.0000e-04
## Epoch 264/500
## 90/90 - 0s - 2ms/step - loss: 0.0518 - sparse_categorical_accuracy: 0.9861 - val_loss: 0.1094 - val_sparse_categorical_accuracy: 0.9639 - learning_rate: 1.0000e-04
## Epoch 265/500
## 90/90 - 0s - 1ms/step - loss: 0.0528 - sparse_categorical_accuracy: 0.9806 - val_loss: 0.0981 - val_sparse_categorical_accuracy: 0.9639 - learning_rate: 1.0000e-04
## Epoch 266/500
## 90/90 - 0s - 1ms/step - loss: 0.0499 - sparse_categorical_accuracy: 0.9851 - val_loss: 0.0968 - val_sparse_categorical_accuracy: 0.9667 - learning_rate: 1.0000e-04
## Epoch 267/500
## 90/90 - 0s - 2ms/step - loss: 0.0483 - sparse_categorical_accuracy: 0.9872 - val_loss: 0.0983 - val_sparse_categorical_accuracy: 0.9681 - learning_rate: 1.0000e-04
## Epoch 268/500
## 90/90 - 0s - 2ms/step - loss: 0.0470 - sparse_categorical_accuracy: 0.9875 - val_loss: 0.0974 - val_sparse_categorical_accuracy: 0.9681 - learning_rate: 1.0000e-04
## Epoch 269/500
## 90/90 - 0s - 1ms/step - loss: 0.0503 - sparse_categorical_accuracy: 0.9858 - val_loss: 0.1045 - val_sparse_categorical_accuracy: 0.9626 - learning_rate: 1.0000e-04
## Epoch 270/500
## 90/90 - 0s - 2ms/step - loss: 0.0455 - sparse_categorical_accuracy: 0.9896 - val_loss: 0.1009 - val_sparse_categorical_accuracy: 0.9653 - learning_rate: 1.0000e-04
## Epoch 271/500
## 90/90 - 0s - 2ms/step - loss: 0.0487 - sparse_categorical_accuracy: 0.9854 - val_loss: 0.0957 - val_sparse_categorical_accuracy: 0.9667 - learning_rate: 1.0000e-04
## Epoch 272/500
## 90/90 - 0s - 1ms/step - loss: 0.0485 - sparse_categorical_accuracy: 0.9830 - val_loss: 0.1159 - val_sparse_categorical_accuracy: 0.9626 - learning_rate: 1.0000e-04
## Epoch 273/500
## 90/90 - 0s - 2ms/step - loss: 0.0492 - sparse_categorical_accuracy: 0.9858 - val_loss: 0.1097 - val_sparse_categorical_accuracy: 0.9639 - learning_rate: 1.0000e-04
## Epoch 274/500
## 90/90 - 0s - 2ms/step - loss: 0.0469 - sparse_categorical_accuracy: 0.9865 - val_loss: 0.0970 - val_sparse_categorical_accuracy: 0.9653 - learning_rate: 1.0000e-04
## Epoch 275/500
## 90/90 - 0s - 1ms/step - loss: 0.0446 - sparse_categorical_accuracy: 0.9878 - val_loss: 0.1164 - val_sparse_categorical_accuracy: 0.9653 - learning_rate: 1.0000e-04
## Epoch 276/500
## 90/90 - 0s - 2ms/step - loss: 0.0488 - sparse_categorical_accuracy: 0.9826 - val_loss: 0.0977 - val_sparse_categorical_accuracy: 0.9681 - learning_rate: 1.0000e-04
## Epoch 277/500
## 90/90 - 0s - 2ms/step - loss: 0.0487 - sparse_categorical_accuracy: 0.9861 - val_loss: 0.1015 - val_sparse_categorical_accuracy: 0.9695 - learning_rate: 1.0000e-04
## Epoch 278/500
## 90/90 - 0s - 2ms/step - loss: 0.0500 - sparse_categorical_accuracy: 0.9837 - val_loss: 0.1040 - val_sparse_categorical_accuracy: 0.9681 - learning_rate: 1.0000e-04
## Epoch 279/500
## 90/90 - 0s - 2ms/step - loss: 0.0497 - sparse_categorical_accuracy: 0.9840 - val_loss: 0.1011 - val_sparse_categorical_accuracy: 0.9667 - learning_rate: 1.0000e-04
## Epoch 280/500
## 90/90 - 0s - 2ms/step - loss: 0.0482 - sparse_categorical_accuracy: 0.9833 - val_loss: 0.0968 - val_sparse_categorical_accuracy: 0.9667 - learning_rate: 1.0000e-04
## Epoch 281/500
## 90/90 - 0s - 2ms/step - loss: 0.0463 - sparse_categorical_accuracy: 0.9872 - val_loss: 0.1021 - val_sparse_categorical_accuracy: 0.9667 - learning_rate: 1.0000e-04
## Epoch 282/500
## 90/90 - 0s - 2ms/step - loss: 0.0456 - sparse_categorical_accuracy: 0.9868 - val_loss: 0.0966 - val_sparse_categorical_accuracy: 0.9653 - learning_rate: 1.0000e-04
## Epoch 283/500
## 90/90 - 0s - 2ms/step - loss: 0.0498 - sparse_categorical_accuracy: 0.9847 - val_loss: 0.0979 - val_sparse_categorical_accuracy: 0.9626 - learning_rate: 1.0000e-04
## Epoch 284/500
## 90/90 - 0s - 2ms/step - loss: 0.0513 - sparse_categorical_accuracy: 0.9830 - val_loss: 0.0987 - val_sparse_categorical_accuracy: 0.9598 - learning_rate: 1.0000e-04
## Epoch 285/500
## 90/90 - 0s - 2ms/step - loss: 0.0492 - sparse_categorical_accuracy: 0.9847 - val_loss: 0.1071 - val_sparse_categorical_accuracy: 0.9681 - learning_rate: 1.0000e-04
## Epoch 286/500
## 90/90 - 0s - 2ms/step - loss: 0.0463 - sparse_categorical_accuracy: 0.9847 - val_loss: 0.1222 - val_sparse_categorical_accuracy: 0.9570 - learning_rate: 1.0000e-04
## Epoch 287/500
## 90/90 - 0s - 2ms/step - loss: 0.0460 - sparse_categorical_accuracy: 0.9868 - val_loss: 0.1056 - val_sparse_categorical_accuracy: 0.9639 - learning_rate: 1.0000e-04
## Epoch 288/500
## 90/90 - 0s - 2ms/step - loss: 0.0466 - sparse_categorical_accuracy: 0.9865 - val_loss: 0.1018 - val_sparse_categorical_accuracy: 0.9653 - learning_rate: 1.0000e-04
## Epoch 289/500
## 90/90 - 0s - 2ms/step - loss: 0.0475 - sparse_categorical_accuracy: 0.9865 - val_loss: 0.1107 - val_sparse_categorical_accuracy: 0.9639 - learning_rate: 1.0000e-04
## Epoch 290/500
## 90/90 - 0s - 1ms/step - loss: 0.0498 - sparse_categorical_accuracy: 0.9851 - val_loss: 0.0968 - val_sparse_categorical_accuracy: 0.9681 - learning_rate: 1.0000e-04
## Epoch 291/500
## 90/90 - 0s - 1ms/step - loss: 0.0452 - sparse_categorical_accuracy: 0.9868 - val_loss: 0.0979 - val_sparse_categorical_accuracy: 0.9667 - learning_rate: 1.0000e-04
## Epoch 292/500
## 90/90 - 0s - 2ms/step - loss: 0.0534 - sparse_categorical_accuracy: 0.9833 - val_loss: 0.1035 - val_sparse_categorical_accuracy: 0.9653 - learning_rate: 1.0000e-04
## Epoch 293/500
## 90/90 - 0s - 2ms/step - loss: 0.0507 - sparse_categorical_accuracy: 0.9840 - val_loss: 0.1129 - val_sparse_categorical_accuracy: 0.9639 - learning_rate: 1.0000e-04
## Epoch 294/500
## 90/90 - 0s - 2ms/step - loss: 0.0474 - sparse_categorical_accuracy: 0.9847 - val_loss: 0.1040 - val_sparse_categorical_accuracy: 0.9639 - learning_rate: 1.0000e-04
## Epoch 295/500
## 90/90 - 0s - 2ms/step - loss: 0.0532 - sparse_categorical_accuracy: 0.9826 - val_loss: 0.0991 - val_sparse_categorical_accuracy: 0.9667 - learning_rate: 1.0000e-04
## Epoch 296/500
## 90/90 - 0s - 2ms/step - loss: 0.0499 - sparse_categorical_accuracy: 0.9830 - val_loss: 0.1021 - val_sparse_categorical_accuracy: 0.9584 - learning_rate: 1.0000e-04
## Epoch 297/500
## 90/90 - 0s - 2ms/step - loss: 0.0504 - sparse_categorical_accuracy: 0.9840 - val_loss: 0.0987 - val_sparse_categorical_accuracy: 0.9626 - learning_rate: 1.0000e-04
## Epoch 298/500
## 90/90 - 0s - 2ms/step - loss: 0.0491 - sparse_categorical_accuracy: 0.9851 - val_loss: 0.0969 - val_sparse_categorical_accuracy: 0.9667 - learning_rate: 1.0000e-04
## Epoch 299/500
## 90/90 - 0s - 2ms/step - loss: 0.0442 - sparse_categorical_accuracy: 0.9872 - val_loss: 0.1308 - val_sparse_categorical_accuracy: 0.9542 - learning_rate: 1.0000e-04
## Epoch 300/500
## 90/90 - 0s - 2ms/step - loss: 0.0447 - sparse_categorical_accuracy: 0.9875 - val_loss: 0.1038 - val_sparse_categorical_accuracy: 0.9681 - learning_rate: 1.0000e-04
## Epoch 301/500
## 90/90 - 0s - 2ms/step - loss: 0.0475 - sparse_categorical_accuracy: 0.9858 - val_loss: 0.0988 - val_sparse_categorical_accuracy: 0.9612 - learning_rate: 1.0000e-04
## Epoch 302/500
## 90/90 - 0s - 2ms/step - loss: 0.0450 - sparse_categorical_accuracy: 0.9875 - val_loss: 0.1110 - val_sparse_categorical_accuracy: 0.9681 - learning_rate: 1.0000e-04
## Epoch 303/500
## 90/90 - 0s - 2ms/step - loss: 0.0446 - sparse_categorical_accuracy: 0.9889 - val_loss: 0.0995 - val_sparse_categorical_accuracy: 0.9667 - learning_rate: 1.0000e-04
## Epoch 304/500
## 90/90 - 0s - 2ms/step - loss: 0.0482 - sparse_categorical_accuracy: 0.9861 - val_loss: 0.1003 - val_sparse_categorical_accuracy: 0.9667 - learning_rate: 1.0000e-04
## Epoch 305/500
## 90/90 - 0s - 2ms/step - loss: 0.0473 - sparse_categorical_accuracy: 0.9875 - val_loss: 0.1027 - val_sparse_categorical_accuracy: 0.9653 - learning_rate: 1.0000e-04
## Epoch 305: early stopping

Evaluate model on test data

model <- load_model("best_model.keras")

results <- model |> evaluate(x_test, y_test)

## 42/42 - 1s - 15ms/step - loss: 0.0986 - sparse_categorical_accuracy: 0.9682

str(results)

## List of 2
##  $ loss                       : num 0.0986
##  $ sparse_categorical_accuracy: num 0.968

cat(
  "Test accuracy: ", results$sparse_categorical_accuracy, "\n",
  "Test loss: ", results$loss, "\n",
  sep = ""
)

## Test accuracy: 0.9681818
## Test loss: 0.09857567

Plot the model’s training history

plot(history)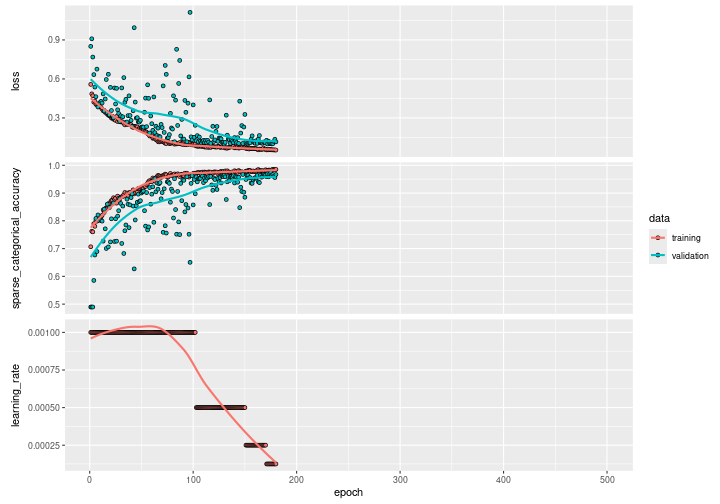

Plot of Training History Metrics

Plot just the training and validation accuracy:

plot(history, metric = "sparse_categorical_accuracy") +
  # scale x axis to actual number of epochs run before early stopping
  ggplot2::xlim(0, length(history$metrics$loss))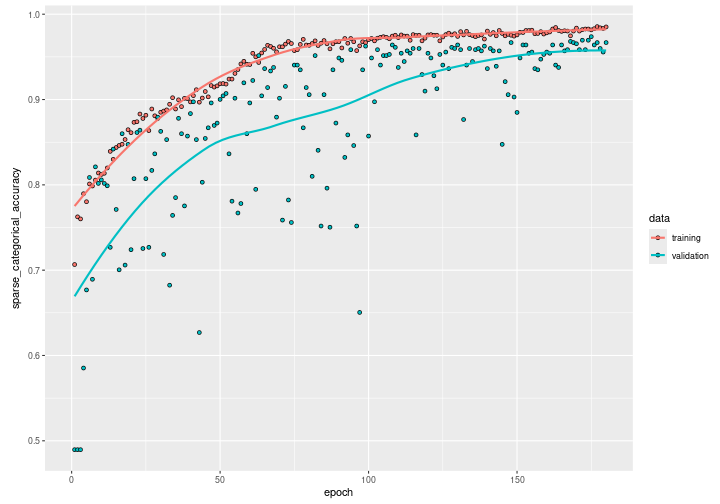

Plot of Accuracy During Training

We can see how the training accuracy reaches almost 0.95 after 100 epochs. However, by observing the validation accuracy we can see how the network still needs training until it reaches almost 0.97 for both the validation and the training accuracy after 200 epochs. Beyond the 200th epoch, if we continue on training, the validation accuracy will start decreasing while the training accuracy will continue on increasing: the model starts overfitting.